Tính chất tứ giác nội tiếp? Các dạng bài tập về tính chất nội tiếp

Chuyên đề tính chất tứ giác nội tiếp là một bài học quan trọng nằm trong chương trình toán lớp 9. Tuy nhiên không phải bạn học sinh nào cũng nắm vững kiến thức này. Tính chất tứ giác nội tiếp là gì? Chúng Tôi sẽ cùng bạn hệ thống lại kiến thức và ôn tập kĩ hơn nhé!

Tứ giác nội tiếp là gì?

Tứ giác nội tiếp là một tứ giác mà cả bốn đỉnh đều nằm trên một đường tròn. Đường tròn này được gọi là đường tròn ngoại tiếp, và các đỉnh của tứ giác được gọi là đồng viên. Tâm và bán kính đường tròn lần lượt được gọi là tâm đường tròn ngoại tiếp và bán kính đường tròn ngoại tiếp.

Thông thường tứ giác nội tiếp là tứ giác lồi, nhưng cũng tồn tại các tứ giác nội tiếp lõm. Các công thức trong bài viết sẽ chỉ áp dụng cho tứ giác lồi.

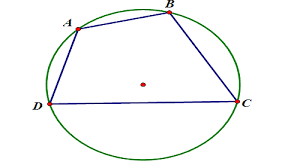
Tính chất tứ giác nội tiếp

Tính chất 1: Trong một tứ giác nội tiếp ABCD, các tâm đường tròn nội tiếp M1, M2, M3, M4 của các tam giác DAB, ABC, BCD, và CDA là 4 đỉnh của một hình chữ nhật. Đây là phát biểu của định lý Nhật Bản về tứ giác nội tiếp.

Ngoài ra, các trực tâm của bốn tam giác trên là đỉnh của một tứ giác nội tiếp đồng dạng với tứ giác ABCD, và các trọng tâm của bốn tam giác này cũng tạọ nên một tứ giác nội tiếp.

Tính chất 2: Trong một tứ giác nội tiếp ABCD với tâm ngoại tiếp O, gọi P là giao điểm của AC và BD. Ta có số đo góc APB là trung bình cộng của số đo hai góc AOB và COD. Đây là một kết quả trực tiếp suy ra từ đinh lý góc trong và định lý góc ngoài.

Tính chất 3: Không tồn tại một tứ giác nội tiếp có diện tích và số đo bốn cạnh khác nhau đều là số hữu tỉ.

Tính chất 4: Nếu hai cặp cạnh đối của tứ giác cắt nhau tại E và F, thì tia phân giác của hai góc trong có đỉnh E và F là vuông góc với nhau

Đặc điểm tứ giác nội tiếp

Sau đây là đặc điểm của một tứ giác nội tiếp:

• Tâm đường tròn ngoại tiếp của tứ giác nội tiếp là giao điểm của các đường trung trực của các cạnh.
• Nếu tứ giác nội tiếp có 2 góc đối diện là góc vuông thì tâm đường tròn ngoại tiếp là trung điểm của đường chéo nối liền 2 đỉnh kia.
• Nếu tứ giác nội tiếp có 2 góc vuông cùng nhìn 1 cạnh thì tâm đường tròn ngoại tiếp là trung điểm của cạnh mà 2 góc cùng nhìn.

Các công thức liên quan tứ giác nội tiếp

Công thức tính diện tích tứ giác nội tiếp

Công thức tính diện tích hình tứ giác thuộc các hình cụ thể như sau (Kí hiệu là S)

Tính diện tích hình tứ giác thường:

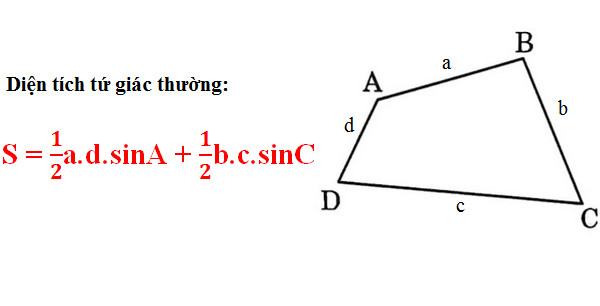
Trong đó: a, b, c, d là độ dài cạnh bên

Công thức tính đường chéo tứ giác nội tiếp

Trong một tứ giác nội tiếp có bốn đỉnh A, B, C, D và cạnh a = AB, b = BC, c = CD, d = DA, độ dài đường chéo p = AC và q = BD có thể được cho bởi công thức

p = ( a c + b d ) ( a d + b c ) a b + c d {displaystyle p={sqrt {frac {(ac+bd)(ad+bc)}{ab+cd}}}} and q = ( a c + b d ) ( a b + c d ) a d + b c {displaystyle q={sqrt {frac {(ac+bd)(ab+cd)}{ad+bc}}}}

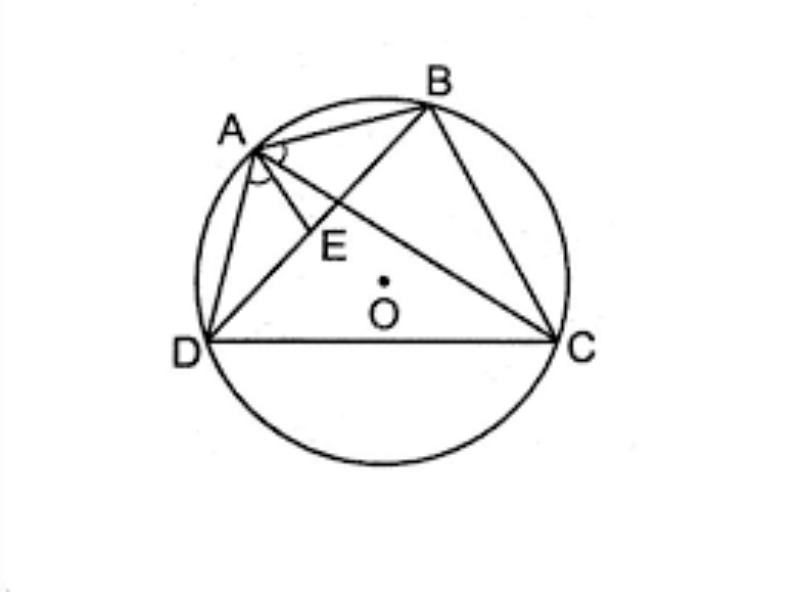
Công thức các góc và liên hệ giữa các góc trong tứ giác

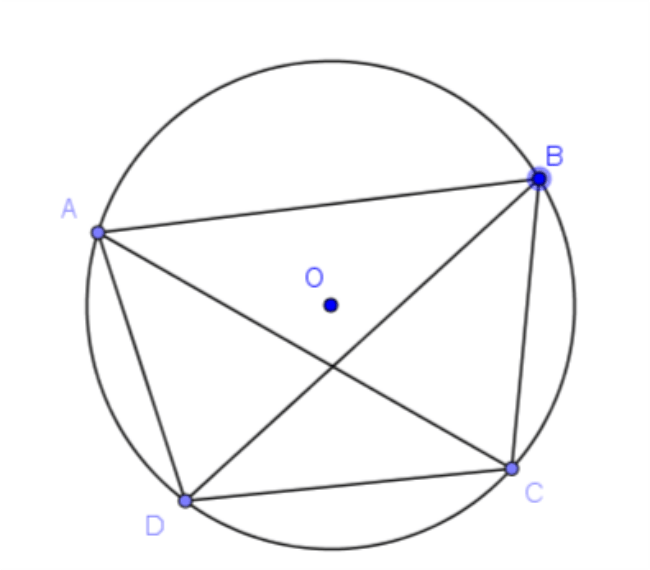
Trong  một tứ giác nội tiếp, tổng số đo hai góc đối diện bằng 180∘180∘. Nếu một tứ giác có tổng số đo hai góc đối diện bằng 180∘180∘ thì tứ giác đó nội tiếp được đường tròn.

Ví dụ: Trong hình 11 , tứ giác nội tiếp ABCDABCD có ˆA+ˆC=180∘;ˆB+ˆD=180∘A^+C^=180∘;B^+D^=180∘.

Chú ý : Trong các hình đã học thì hình chữ nhật, hình vuông, hình thang cân nội tiếp được đường tròn.

Công thức Parameshvara về bán kính đường tròn ngoại tiếp

Một tứ giác nội tiếp có các cạnh a, b, c, d và nửa chu vi s; có độ dài bán kính đường tròn ngoại tiếp xác định bởi:[11][18]

R = 1 4 ( a b + c d ) ( a c + b d ) ( a d + b c ) ( s − a ) ( s − b ) ( s − c ) ( s − d ) . {displaystyle R={frac {1}{4}}{sqrt {frac {(ab+cd)(ac+bd)(ad+bc)}{(s-a)(s-b)(s-c)(s-d)}}}.}. Công thức được tìm ra vào thế kỷ XV bởi nhà toán học Ấn Độ Vatasseri Parameshvara.

Sử dụng công thức Brahmagupta, công thức Parameshvara có thể được phát biểu lại là:

4 K R = ( a b + c d ) ( a c + b d ) ( a d + b c ) {displaystyle 4KR={sqrt {(ab+cd)(ac+bd)(ad+bc)}}}trong đó K là diện tích tứ giác nội tiếp.

Các dạng bài toán về tính chất tứ giác nội tiếp

Dạng 1. Chứng minh tứ giác nội tiếp

Phương pháp giải: Để chứng minh tứ giác nội tiếp, ta có thể sử dụng một trong các cách sau:

• Cách 1. Chứng minh tứ giác có tổng hai góc đôì bằng 180°.
• Cách 2. Chứng minh tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc α.
• Cách 3. Chứng minh tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện.
• Cách 4. Tìm được một điểm cách đều 4 đỉnh của tứ giác.

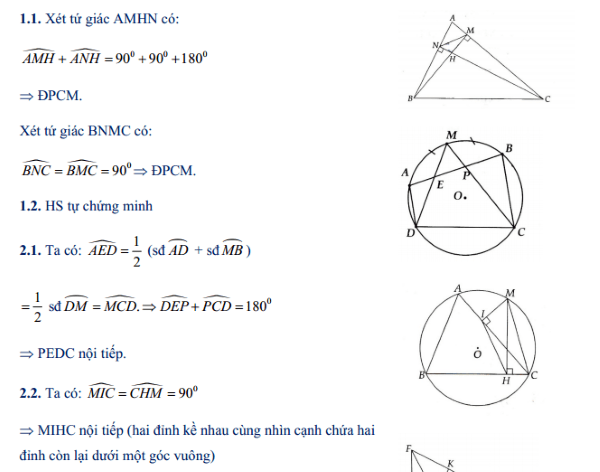
Bài 1.1: Cho tam giác ABC nhọn, đường cao BM và CN cắt nhau tại H. Chứng minh các tứ giác AMHN và BNMC là những tứ giác nội tiếp.

Bài 1.2: Cho điểm A nằm ngoài đường tròn (O), qua A kẻ hai tiếp tuyến AB và AC với đường tròn (B, C là tiếp điểm). Chứng minh tứ giác ABOC là tứ giác nội tiếp.

Bài 2.1: Cho tứ giác ABCD nội tiếp (O), M là điểm chính giữa của cung AB. Nối M với D, M với C cắt AB lần lượt ở E và P. Chứng minh PEDC là tứ giác nội tiếp.

Bài 2.2: Cho tam giác ABC nhọn nội tiếp đường tròn (O). M là điểm thuộc đường tròn. Vẽ MH vuông góc với BC tại H, vẽ MI vuông góc với AC. Chứng minh MIHC là tứ giác nội tiếp.

Lời giải:

Dạng 2:  Sử dụng tứ giác nội tiếp để chứng minh các góc bằng nhau, các đoạn thẳng bằng nhau, các đường thẳng song song hoặc đồng quy, các tam giác đồng dạng…

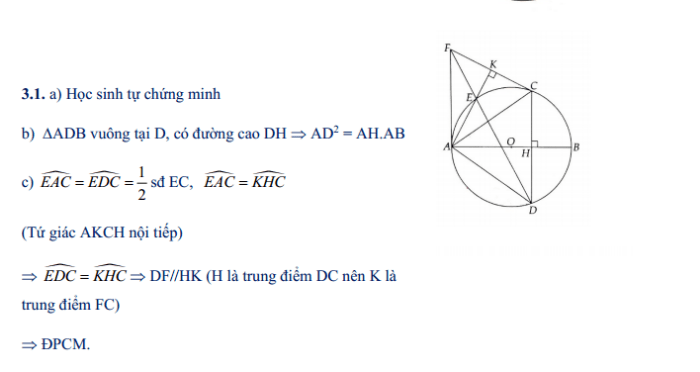
Bài tập 3.1. Cho đường tròn (O) đường kính AB. Gọi H là điểm nằm giữa O và B. Kẻ dây CD vuông góc với AB tại H. Trên cung nhỏ AC lấy điểm E, kẻ CK vuông góc AE tại K. Đường thẳng DE cắt CK tại F. Chứng minh:

a) Tứ giác AHCK là tứ giác nội tiếp;

b) AH.AB = AD2

c) Tam giác ACE là tam giác cân.

Lời giải:

Bài tập 3.2. Cho nửa (O) đường kính AB. Lấy M thuộc OA (M không trùng O và A). Qua M vẽ đường thẳng d vuông góc với AB. Trên d lấy N sao cho ON > R. Nối NB cắt (O) tại C. Kẻ tiếp tuyến NE với (O) (E là tiếp điểm, E và A cùng thuộc nửa mặt phẳng bờ d). Chứng minh:

a) Bốn điểm O, E, M, N cùng thuộc một đường tròn;

b) NE2 = NC.NB;

c) góc NEH = góc NME (H là giao điểm của AC và d);

d) NF là tiếp tuyến (O) với F là giao điểm của HE và (O)

Lời giải:

Bài viết trên của Chúng Tôi đã chia sẻ đến bạn chủ đề tính chất tứ giác nội tiếp và các dạng bài tập cơ bản liên quan đến bài toán này. Chúc các bạn học tập tốt. Hẹn gặp lại ở bài viết sau!