Bạn đang xem bài viết Tính chất hình chữ nhật? 4 dấu hiệu nhận biết HCN tại thcshuynhphuoc-np.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Hình chữ nhật là một hình hình học phổ biến trong toán học và vật lý. Được biết đến với các tính chất đặc trưng, hình chữ nhật là tạo hình tương đối đơn giản nhưng lại mang trong mình một số đặc điểm đáng chú ý. Để nhận biết một hình có phải là hình chữ nhật hay không, ta có thể xác định qua 4 dấu hiệu sau:
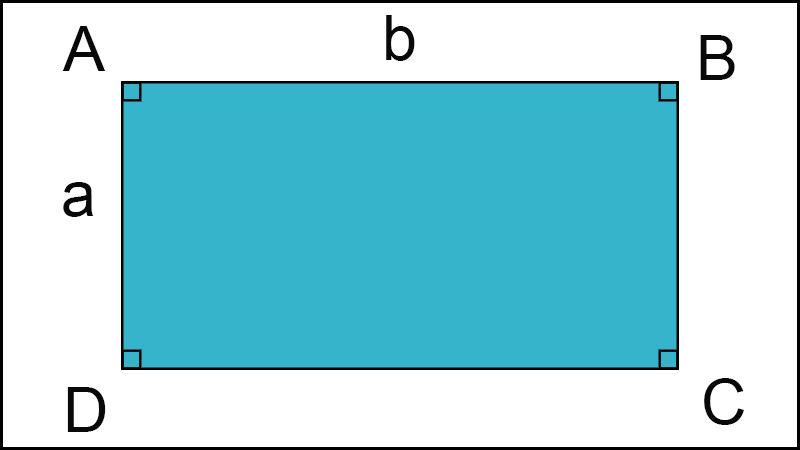
1. Các góc trong hình chữ nhật đều là góc vuông: Tính chất đặc trưng nhất của hình chữ nhật chính là các góc bên trong luôn có độ lớn là 90 độ. Điều này đảm bảo rằng các đường thẳng trong hình chữ nhật gặp nhau đều tạo thành các góc vuông.
2. Các cạnh đối diện của hình chữ nhật có độ dài bằng nhau: Điều này có nghĩa là cặp cạnh đối diện AB và CD trong hình chữ nhật sẽ có độ dài bằng nhau. Điều này làm nổi bật tính đối xứng của hình chữ nhật và tạo ra nhiều ứng dụng trong thực tế.
3. Hai đường chéo của hình chữ nhật giao nhau tại một điểm giữa: Đường chéo AC và BD trong hình chữ nhật sẽ giao nhau tại một điểm duy nhất, gọi là điểm giao của đường chéo. Điều này cho phép ta xác định một thông số quan trọng của hình chữ nhật – độ dài các đường chéo.
4. Các cạnh của hình chữ nhật song song và vuông góc với nhau: Các cạnh bên của hình chữ nhật luôn song song và vuông góc với cạnh đối diện của nó. Điều này đảm bảo rằng các đường thẳng trong hình chữ nhật không giao nhau và đồng thời tạo nên tính chất đối xứng cho hình học này.
Với những đặc điểm nổi bật như vậy, nhận biết một hình có phải là hình chữ nhật hay không trở nên dễ dàng hơn.
Có thể bạn không biết, cứ 10 đồ vật xung quanh chúng ta thì có hơn một nửa là có hình chữ nhật. Vậy các tính chất hình chữ nhật là gì? Dựa vào tính chất hình chữ nhật chúng ta có thể xây dựng các nội dung gì? Tất cả sẽ được Chúng Tôi giải đáp ngay sau đây!
Hình chữ nhật là hình gì?
Định nghĩa hình chữ nhật là gì?
Hình chữ nhật trong hình học là một tứ giác lồi có 4 góc vuông. Hoặc có thể nói hình chữ nhật là hình bình hành có bốn góc vuông.
Từ “nhật” bắt nguồn từ kí tự 日 (nhật) trong tiếng Nhật. Hình chữ nhật và các tính chất hình chữ nhật là một trong những kiến thức nền tảng trong toán học.

Dấu hiệu nhận biết hình chữ nhật
Sau khi xác định được hình chữ nhật, người xem sẽ nắm rõ hơn về các tính chất hình chữ nhật. Có 4 dấu hiệu cơ bản và quan trọng nhất của hình chữ nhật như sau:
- Tứ giác có ba góc vuông là hình chữ nhật.
- Hình thang cân có một góc vuông là hình chữ nhật.
- Hình bình hành có một góc vuông là hình chữ nhật.
- Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
Có rất nhiều bài toán theo chiều hướng “ngược”. Chính là dựa vào những dấu hiệu để xác định hình dạng ban đầu. Để làm tốt được dạng bài đó, thì dấu hiệu nhận biết kết hợp với tính chất hình chữ nhật là một cách không thể bỏ qua.
Tính chất hình chữ nhật
Tính chất hình chữ nhật gồm 4 điều cần ghi nhớ. Những tính chất này không quá phức tạp nhưng đây sẽ là yếu tố quan trọng nhất trong các bài toán hình học.
- Trong hình chữ nhật, hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
- Hình chữ nhật có tất cả các tính chất của hình thang cân và hình bình hành.
- Hình chữ nhật gồm các đường chéo cắt nhau tạo thành 4 tam giác cân.
- Trong tam giác vuông chia hình chữ nhật ra một nửa, đường trung tuyến ứng với cạnh huyền thì bằng nửa cạnh huyền.
Các công thức liên quan đến hình chữ nhật
Công thức tính diện tích hình chữ nhật
Diện tích chính là đại lượng biểu thị phạm vi của hình trong mặt phẳng. So với một đa giác thông thường, công thức diện tích hình chữ nhật đơn giản hơn rất nhiều. Có thể có 4 tính chất hình chữ nhật nhưng chỉ có duy nhất một công thức tính hình chữ nhật.
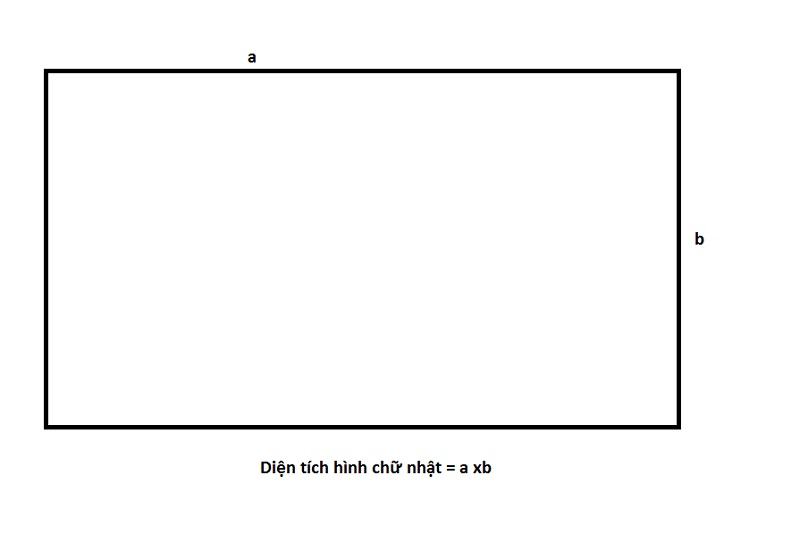
Với một hình chữ nhật có chiều dài b và chiều rộng a thì diện tích của hình chữ nhật S này được xác định với công thức: S = b*a
Công thức tính chu vi hình chữ nhật
Chu vi được xem là độ dài của đường bao quanh một hình hai chiều. Một tứ giác được xác định chu vi với tổng độ dài các cạnh của nó.
Hình chữ nhật là hình có 2 cạnh song song có cùng độ dài. Do đó chu vi hình chữ nhật (CV) với a (chiều dài), b (chiều rộng) được xác định với công thức như sau:CV= (a+b)*2

Công thức tính đường chéo hình chữ nhật
Đường chéo hình chữ nhật là cạnh của 2 tam giác vuông chia đều hình chữ nhật ra làm hai. Do đó để tính được đường chéo hình chữ nhật, ta có thể xem nó như cạnh huyền của tam giác vuông.
Áp dụng định lý Pytago trong một tam giác vuông. Trong đó, 2 cạnh lần lượt là chiều dài (d) và chiều rộng (r) của hình chữ nhật. Ta có công thức tính cạnh huyền c (đường chéo hình chữ nhật) của tam giác đó như sau: c^2 = d^2 + r^2
Nội dung liên quan đến hình chữ nhật
Định nghĩa, tính chất đường chéo hình chữ nhật
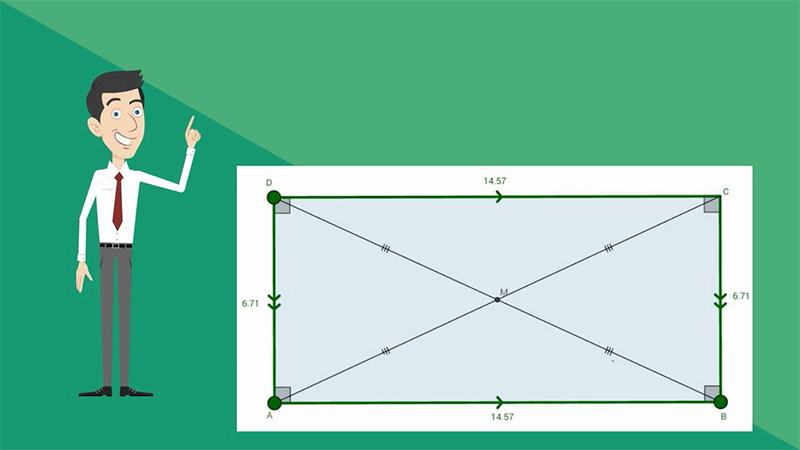
Đường chéo trong hình chữ nhật là đường thẳng nối hai góc đối diện trong hình chữ nhật. Độ dài hai đường chéo trong hình chữ nhật có độ dài bằng nhau.
Hai đường chéo cắt nhau tại trung điểm của mỗi đường, cắt nhau tạo ra 4 tam giác cân. Hai đường chéo của hình chữ nhật vuông góc với nhau là hình vuông.
Từ đó, tính chất đường chéo hình chữ nhật còn được xem là một kiến thức “con” của tính chất hình chữ nhật.
Định nghĩa tâm đối xứng hình vuông
Hình vuông là hình chữ nhật với 4 cạnh bằng nhau. Hay có thể nói, những tính chất hình chữ nhật thì hình vuông đều có.
Hình chữ nhật có tâm đối xứng là giao điểm của hai đường chéo. Hình vuông cũng vậy, tâm của hình vuông cũng chính là giao điểm của hai đường chéo.
Ngoài ra do có các cạnh bằng nhau nên đường trung bình cũng chính là các trục đối xứng của hình vuông
Định nghĩa đường tròn ngoại tiếp hình chữ nhật
Đường tròn ngoại tiếp của một đa giác là đường tròn đi qua tất cả các đỉnh của đa giác đó. Hình chữ nhật có tâm đối xứng là giao điểm của hai đường chéo. Khoảng cách từ tâm hình chữ nhật đến các đỉnh chính là bán kính của đường tròn ngoại tiếp hình chữ nhật đó.
Những câu hỏi dựa trên tính chất hình chữ nhật được dùng rất nhiều trong các đề thi. Bên cạnh đó, các bài toán về đường tròn ngoại tiếp được xem là dạng toán nâng cao từ các tính chất hình chữ nhật.
Câu hỏi thường gặp về hình chữ nhật
Hình chữ nhật có phải là hình vuông không?
Hình vuông được định nghĩa là một tứ giác đều với các cạnh bằng nhau và các góc bằng nhau. Trong khi đó hình chữ nhật có cặp cạnh vuông góc với nhau sẽ không bằng nhau.
Để một hình chữ nhật được xem là hình vuông, hình chữ nhật đó cần phải có hai cạnh kề bằng nhau. Không chỉ vậy, hai đường chéo còn phải vuông góc và có một đường chéo là phân giác của một góc.
Hình vuông có khác gì so với hình chữ nhật?
Tuy những tính chất hình chữ nhật đều giống với hình vuông, song vẫn tồn tại những điểm khác nhau như sau:
- So với hình chữ nhật, hình vuông có các cạnh đều bằng nhau.
- Các đường chéo của hình vuông sẽ vuông góc với nhau và tạo ra một tam giác vuông cân.
- Giao điểm của các đường phân giác, trung tuyến, trung trực đều trùng tại một điểm.
Một số bài tập tham khảo
Chúng Tôi sẽ đưa đến các bạn một số bài tập tham khảo dựa trên những công thức đã đề cập ở trên như sau:
Bài tập 1
Cho hình chữ nhật ABCD có độ dài chiều dài và chiều rộng của hình chữ nhật lần lượt là 7cm và 5cm. Tính diện tích hình chữ nhật?
Bài giải
Áp dụng công thức ta có, diện tích hình chữ nhật ABCD là:
S = 7.5 =35 (cm2)
Bài tập 2
Cho hình chữ nhật ABCD có độ dài chiều dài và chiều rộng của hình chữ nhật lần lượt là 7cm và 5cm. Tính chu vi hình chữ nhật?
Bài giải
Áp dụng công thức ta có, chu vi hình chữ nhật ABCD là:
S = 2( 7 + 5 ) = 24 (cm)
Bài tập 3
Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC, E là điểm đối xứng với H qua I. Chứng minh tứ giác AHCE là hình chữ nhật.
Bài giải
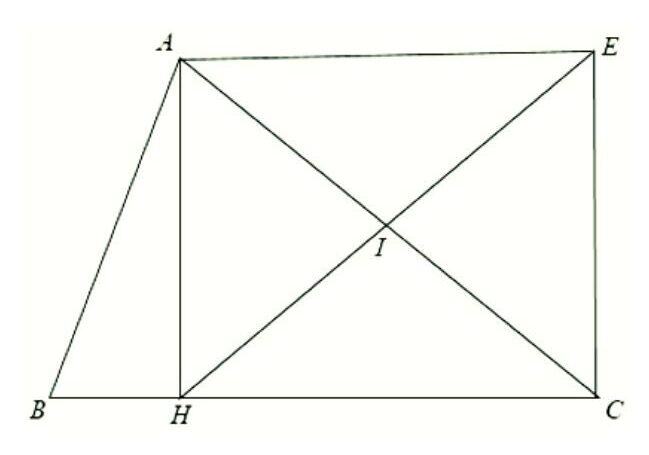
Trong Δ AHC vuông có I là trung điểm của AC
⇒ HE là đường trung tuyến của Δ AHC.
⇒ HI = 1/2AC = AI = IC.
Mà E đối xứng với H qua I ⇒ HI = IE.
Khi đó ta có HI = IE = AI = IC.
Xét Δ HCE có CI là đường trung tuyến ứng với cạnh HE
mà CI = 1/2HE ⇒ Δ HCE vuông tại C.
Tương tự xét với Δ AHE,Δ AEC đều là các tam giác vuông tại A, E.
Xét tứ giác AHCE có EAHˆ = AHCˆ = HCEˆ = CEAˆ = 90 độ
Theo tính chất hình chữ nhật ⇒ AHCE là hình chữ nhật.
Có thể nhận thấy tính chất hình chữ nhật thật ra rất dễ nhớ. Nếu bạn nhận biết rõ những dấu hiệu và các công thức liên quan, những bài toán hình học sẽ chẳng làm khó được bạn. Đừng quên bổ sung kiến thức cùng Chúng Tôi trong các bài viết sau nhé!
Như vậy, tính chất hình chữ nhật là một chủ đề quan trọng trong học hình học cơ bản. Hình chữ nhật là một hình học phẳng có bốn cạnh, hai cạnh ngang đều song song và có cùng độ dài, hai cạnh dọc cũng song song và có cùng độ dài. Tính chất nổi bật của hình chữ nhật gồm có:
1. Có tổng độ dài các cạnh đối diện bằng nhau: Đây là một đặc điểm quan trọng của hình chữ nhật. Tổng độ dài của hai cạnh ngang luôn bằng tổng độ dài của hai cạnh dọc. Điều này cho phép chúng ta dễ dàng tính toán các số liệu liên quan đến hình chữ nhật.
2. Đường chéo bằng nhau và chia hình chữ nhật thành hai tam giác đều nhau: Đường chéo kết nối hai điểm đối xứng của hình chữ nhật có độ dài bằng nhau, cho phép chia hình chữ nhật thành hai nửa có diện tích bằng nhau và hình dạng tương tự nhau.
3. Đối xứng qua đường chéo: Hình chữ nhật có tính chất đối xứng qua đường chéo. Điều này có nghĩa là nếu ta lấy một điểm bất kỳ trong hình chữ nhật và vẽ một đường thẳng qua điểm đó và qua tâm của hình chữ nhật, thì đường thẳng này sẽ cắt cạnh đối xứng tại một điểm có đặc điểm giống hệt với điểm ban đầu.
4. Có tổng diện tích bằng nhân độ dài hai cạnh bên: Tổng diện tích của hình chữ nhật bằng tích của hai cạnh bên. Đây là đặc điểm quan trọng giúp ta tính toán diện tích của hình chữ nhật trong các bài toán liên quan.
Như vậy, từ 4 dấu hiệu nhận biết và tính chất của hình chữ nhật, chúng ta có thể nhận thấy sự đặc biệt và quan trọng của loại hình này trong toán học và thực tế cuộc sống.
Cảm ơn bạn đã xem bài viết Tính chất hình chữ nhật? 4 dấu hiệu nhận biết HCN tại thcshuynhphuoc-np.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Hình chữ nhật
2. Đường chéo
3. Góc vuông
4. Cạnh bằng nhau
5. Diện tích
6. Chu vi
7. Đường kính
8. Tâm đối xứng
9. Đối xứng qua đường thẳng
10. Các cạnh song song
11. Kẻ đường vuông góc
12. Tham gia phép tính
13. Phân tích hình học
14. Định lý Pitago
15. Vị trí tương đối


