Bạn đang xem bài viết Tính chất đường trung trực là gì? Tổng hợp đủ các tính chất tại thcshuynhphuoc-np.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Đường trung trực là thuật ngữ trong hình học góc để chỉ đường thẳng đi qua trung điểm của một đoạn thẳng và đồng thời vuông góc với đoạn thẳng đó. Tính chất đặc trưng của đường trung trực mang lại rất nhiều thông tin quan trọng khi xem xét các hình học góc.
Tính chất đầu tiên của đường trung trực đó là nó luôn đi qua trung điểm của đoạn thẳng mà nó trung trực. Điều này suy ra ngay từ định nghĩa của đường trung trực và khá dễ chứng minh.
Tính chất thứ hai của đường trung trực là nó vuông góc với đoạn thẳng mà nó trung trực. Điều này đồng nghĩa với việc đường trung trực tạo thành một góc vuông với mọi điểm trên đoạn thẳng mà nó trung trực.
Tính chất thứ ba của đường trung trực là nếu hai đường trung trực cắt nhau, thì điểm cắt chính là trung điểm của đoạn thẳng mà hai đường trung trực trung trực. Điều này thể hiện sự độc đáo của đường trung trực, khi nó cũng là nơi mà hai đường trung trực gặp nhau.
Tính chất cuối cùng, và có thể là quan trọng nhất, là đường trung trực còn là trục đối xứng của đoạn thẳng mà nó trung trực. Điều này có nghĩa là mọi điểm trên đoạn thẳng chính nó đều có thể tìm được một điểm cùng khoảng cách nhưng ở phía trái hoặc phía phải đường trung trực.
Những tính chất trên không chỉ giúp chúng ta hiểu về tính chất của đường trung trực mà còn cung cấp thông tin quan trọng trong các bài toán hình học góc, giúp chúng ta dễ dàng xác định vị trí, tính toán khoảng cách và xử lý một số vấn đề liên quan đến không gian 2 chiều.
Có lẽ trong chúng ta ai cũng đã gặp các bài toán liên quan đến đường trung trực rồi phải không nào? Vậy có tất cả bao nhiêu tính chất đường trung trực? Làm thế nào để nhận biết được đâu là đường trung trực? Hãy lướt ngay xuống bài viết dưới đây để cùng Chúng Tôi tìm hiểu ngay nhé!
Đường trung trực là gì?
Trước tiên chúng ta hãy cùng nhau tìm hiểu về khái niệm của đường trung trực các bạn nhé!
Đường trung trực là gì?
Đường trung trực của một đoạn thẳng là đường thẳng đi qua trung điểm của một đoạn thẳng và vuông góc với đoạn thẳng ấy. Đường trung trực được áp dụng vào khá nhiều dạng bài tập khác nhau.
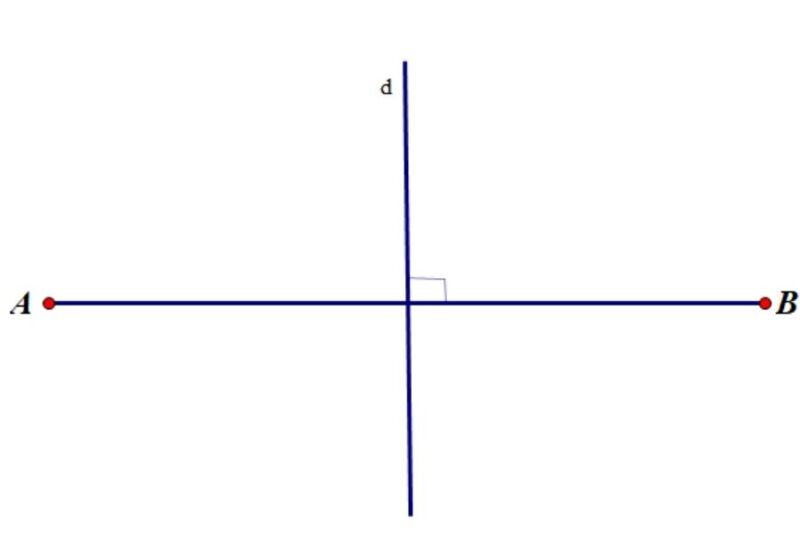
Mỗi đoạn thẳng có bao nhiêu đường trung trực?
Mỗi đoạn thẳng chỉ có duy nhất một đường trung trực. Với mỗi đoạn thẳng bất kì, chỉ có 1 đường thẳng duy nhất vuông góc tại trung điểm của đoạn thẳng đó.
Cách viết phương trình đường trung trực của đoạn thẳng
Chắc hẳn các bạn đều muốn biết cách viết phương trình đường trung trực của một đoạn thẳng phải không? Sau đây là cách phổ biến được nhiều người sử dụng nhất.
Đề bài tổng quát: Cho hai điểm A(xA; yA) và điểm B. Viết phương trình đường trung trực của đoạn thẳng AB. Trước tiên, ta sẽ gọi d là đường trung trực của đoạn thẳng AB. Như vậy đường thẳng (d) sẽ vuông góc AB tại trung điểm C của AB.
Khi đó, phương trình đường thẳng (d) sẽ đi qua M và nhận vectơ AB làm vectơ pháp tuyến. Sau đó chúng ta sẽ viết ngay được phương trình đường thẳng d.

Ví dụ: Cho hai điểm A(1; 0) và điểm B(1; 2). Viết phương trình đường trung trực của đoạn thẳng AB.
Gọi phương trình đường trung trực của AB là d’.
Vì theo đề bài có tọa độ điểm A và B => Ta có: vectơ AB(0; 2) và trung điểm AB là C(1; 1). Vì đường trung trực d’ của đoạn thẳng AB vuông góc với AB tại trung điểm C, từ đó d’ nhận vectơ AB(0; 2) làm vectơ pháp tuyến.
Như vậy, đường trung trực d’ của AB đi qua điểm C(1; 1) và có vectơ pháp tuyến là vectơ AB(0; 2). Vì vậy phương trình đường trung trực của AB là: 0(x – 1) + 2(y – 1) = 0 => y – 1 = 0.
Tính chất đường trung trực
Để tìm hiểu kĩ và sâu hơn về đường trung trực, chúng ta hãy cùng nhau khám phá những tính chất thú vị của đường trung trực nhé!
Tính chất đường trung trực của một đoạn thẳng
Tính chất đường trung trực của một đoạn thẳng bao gồm định lý đảo và định lý thuận. Trước hết, định lý thuận đường trung trực của một đoạn thẳng là điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
Ví dụ:
Theo giả thiết: d là trung trực của AB, M d.
Kết luận: MA = MB (định lý đường trung trực của một đoạn thẳng).
Định lý đảo đường trung trực của một đoạn thẳng là điểm cách đều hai mút của đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.
Ví dụ:
Theo giả thiết: MA = MB.
Kết luận: M ∈ đường trung trực của đoạn thẳng AB (định lý đảo đường trung trực của một đoạn thẳng).
Tính chất ba đường trung trực trong tam giác
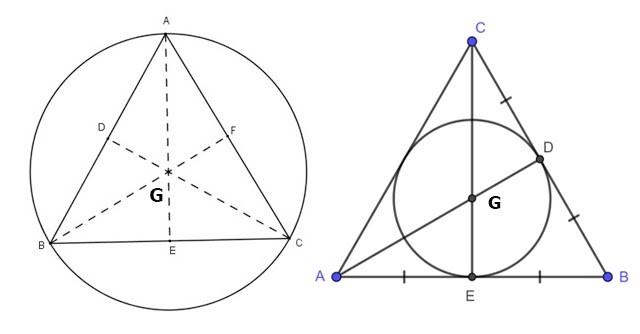
Tính chất ba đường trung trực trong tam giác được phát biểu như sau: Ba đường trung trực của một tam giác cùng đi qua một điểm và điểm này cách đều ba đỉnh của tam giác đó.
Gọi O là giao điểm của ba đường trung trực của tam giác ABC. Đường tròn tâm O sẽ đi qua ba đỉnh A, B, C của tam giác và ta gọi đó là đường tròn ngoại tiếp tam giác ABC.
Chứng minh đường trung trực
Để chứng minh đường trung trực của một đoạn thẳng bất kì, ta có 5 phương pháp chứng minh khác nhau.
- Cách 1: Chứng minh d ⊥ AB tại trung điểm của AB.
- Cách 2: Chứng minh 2 điểm nằm trên d cách đều 2 điểm A và B.
- Cách 3: Áp dụng tính chất đường trung tuyến, đường cao.
- Cách 4: Áp dụng tính chất đối xứng của trục.
- Cách 5: Áp dụng tính chất đoạn nối tâm của 2 đường tròn cắt nhau ở 2 điểm.
Bên trên là các cách phổ biến thường được sử dụng để chứng minh đường trung trực của một đoạn thẳng bất kì. Các bạn có thể áp dụng vào các dạng bài tập khác nhau.
Dạng bài toán về tính chất đường trung trực của một đoạn thẳng
Sau đây là một số dạng toán phổ biến và thường gặp về tính chất đường trung trực của một đoạn thẳng.
Dạng 1: Chứng minh hai đoạn thẳng bằng nhau
Với dạng toán này, chúng ta sẽ sử dụng định lý đường trung trực của một đoạn thẳng: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.
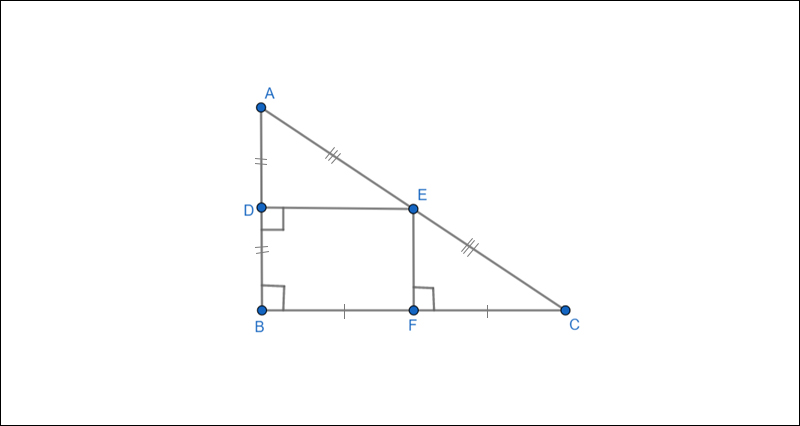
Ví dụ: Cho tam giác ABC vuông tại A, tia phân giác của góc B cắt cạnh AC tại điểm D. Trên cạnh BC, lấy điểm E sao cho: BE = AB. Chứng minh rằng: AD = DE.
Cách giải bài toán như sau:
Xét ΔABD và ΔEBD, ta có:
BD là cạnh chung
BE = AB (theo đề bài)
BD là tia phân giác của góc B => góc ABD = góc DBE
=> ΔABD = ΔEBD (cạnh – góc – cạnh)
=> AD = DE (cạnh tương ứng bằng nhau) (điều phải chứng minh).
Dạng 2: Xác định tâm đường tròn ngoại tiếp tam giác
Với dạng bài này, chúng ta cần phải thực hiện lần lượt 2 bước như sau:
- Áp dụng tính chất giao điểm của ba đường trung trực trong tam giác.
- Kế tiếp ta sẽ sử dụng định lý: Ba đường trung trực của một tam giác cùng đi qua một điểm thì điểm này cách đều ba đỉnh của tam giác đó.
Dạng 3: Đường trung trực trong tam giác cân
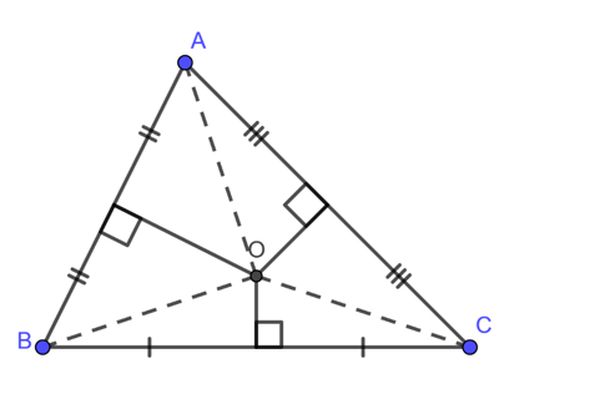
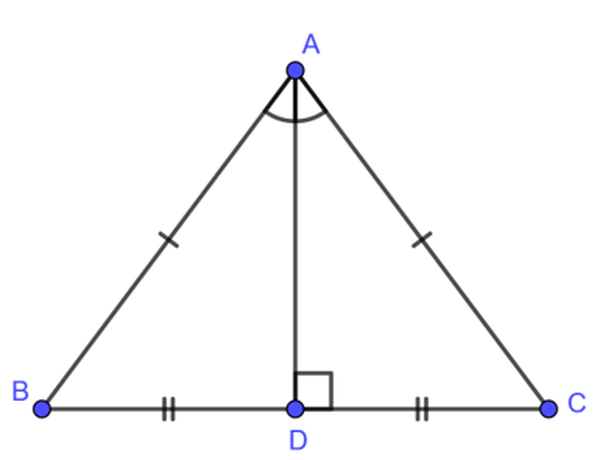
Trước khi làm dạng bài này, chúng ta cần lưu ý một tính chất như sau: Trong tam giác cân, đường trung trực của cạnh đáy đồng thời là đường cao, đường trung tuyến và đường phân giác ứng với cạnh đáy đó.
Ví dụ : Cho tam giác ABC cân tại A, DBC cân tại D và EBC cân tại E có chung đáy BC. Chứng minh ba điểm A, D, E thẳng hàng.
Cách giải:
Vì ΔABC cân tại A (theo đề bài) ⇒ AB = AC
⇒ A nằm trên đường trung trực của BC.
Vì ΔDBC cân tại D ⇒ DB = DC
⇒ D nằm trên đường trung trực của BC.
Vì ΔEBC cân tại E ⇒ EB = EC
⇒ E nằm trên đường trung trực của BC.
Do đó ba điểm A, D, E cùng nằm trên đường trung trực của BC.
Vậy A, D, E thẳng hàng (điều phải chứng minh).
Dạng 4: Chứng minh đường trung trực của một đoạn thẳng
Để chứng minh đường trung trực của một đoạn thẳng bất kì, ta cần sử dụng định nghĩa về đường trung trực.
Ví dụ 1: Chứng minh đường thẳng AB là đường trung trực của đoạn thẳng CD.
A, B là giao điểm của hai cung tròn tâm C, D. Trong đó, hai cung tròn này có cùng bán kính nên ta có:
AC = AD (= bán kính).
BC = BD (= bán kính).
=> Hai điểm A và B cùng thuộc đường trung trực của đoạn thẳng CD.
Vậy AB là đường trung trực của đoạn thẳng CD.
Những bài tập liên quan đến tính chất đường trung trực
Trong chương trình toán học có rất nhiều bài tập liên quan đến tính chất của đường trung trực. Sau đây là một số bài tập cụ thể và thường bắt gặp nhất:
Bài 1: Cho A, B là hai điểm phân biệt và d là đường trung trực của đoạn thẳng AB.
Ta kí hiệu PA là nửa mặt phẳng bờ d có chứa điểm A (không kể đường thẳng d). Gọi là một điểm của PA và M là giao điểm của đường thẳng NB và d. Hãy so sánh NB với NM + MA; từ đó suy ra NA < NB.
Lời giải:
Vì M nằm trên d và d là trung trực của AB nên MA = MB (1).
Vì N ∈ PA nên N và B thuộc hai nửa mặt phẳng khác nhau bờ là đường thẳng d.
⇒ M nằm giữa N và B ⇒ NM + MB = NB (2)
Từ (1) và (2) ⇒ NB = MA + NM.
Trong ∆NMA có : MA + NM > NA (bất đẳng thức tam giác).
⇒ NA < NB.
Bài 2: Cho hai điểm M, N nằm trên đường trung trực của đoạn thẳng AB. Chứng minh ΔAMN = ΔBMN.
Lời giải:
Vì M thuộc đường trung trực của AB.
⇒ MA = MB (định lý thuận về tính chất của các điểm thuộc đường trung trực).
N thuộc đường trung trực của AB.
⇒ NA = NB (định lý thuận về tính chất của các điểm thuộc đường trung trực).
Do đó ΔAMN và ΔBMN có:
AM = BM (cmt)
MN chung
AN = BN (cmt)
⇒ ΔAMN = ΔBMN (c.c.c) (đpcm).
Bài 3: Cho góc xOy bằng 68o, điểm A nằm trong góc đó. Vẽ điểm B sao cho Ox là đường trung trực của AB. Vẽ điểm C sao cho Oy là đường trung trực của AC.
a) So sánh OB và OC.
b) Tính số đo góc BOC.
Lời giải:
a) Ox là đường trung trực của AB.
=> OA = OB ; góc
Oy là đường trung trực của AC.
=> OA = OC ; góc
Do đó OB = OC.
b) góc o

Bài 4: Cho ΔABC có góc A tù. Các đường trung trực của AB, AC cắt nhau tại O và cắt BC theo thứ tự ở D và E. Hỏi ΔABD, ΔACE là tam giác gì?
Lời giải:
Vì D thuộc đường trung trực của AB nên:
DA = DB (tính chất đường trung trực)
=> ΔADB cân tại D.
Vì E thuộc đường trung trực của AC nên:
EA = EC (tính chất đường trung trực)
=> ΔAEC cân tại A.
Dựa vào những cách giải ở phần dạng bài mà chúng mình đã đưa ra, hãy áp dụng vào để tự giải các bài toán thường gặp ở trên nhé! Mong rằng các bạn đã hiểu rõ về tính chất đường trung trực và các dạng bài xoay quanh nó.
Như vậy, sau khi đọc bài viết trên, chắc hẳn các bạn cũng đã hiểu thêm đường phần nào về tính chất đường trung trực rồi phải không nào? Hãy theo dõi Chúng Tôi ngay để cập nhật thêm nhiều thông tin mới mẻ và bổ ích các bạn nhé!
Trong hình học, đường trung trực là một đường chỉ qua trung điểm của một đoạn thẳng và vuông góc với đoạn thẳng đó. Tính chất của đường trung trực rất đặc biệt và đóng vai trò quan trọng trong nhiều bài toán hình học.
Tính chất thứ nhất của đường trung trực là nó là đường thẳng duy nhất đi qua trung điểm của đoạn thẳng. Bất kỳ đường thẳng nào chỉ qua trung điểm đoạn thẳng cũng có tính chất này.
Tính chất thứ hai của đường trung trực là nó là đường thẳng vuông góc với đoạn thẳng này. Điều này có thể được chứng minh bằng cách sử dụng tính chất trực giao của hai đường thẳng. Điều này cho phép ta xác định góc giữa đường trung trực và đoạn thẳng ban đầu là góc vuông.
Tính chất thứ ba của đường trung trực là góc giữa cạnh và đường trung trực bằng góc giữa cạnh và đoạn thẳng. Điều này có thể được chứng minh bằng cách sử dụng tính chất hai góc kề nhau.
Tính chất cuối cùng của đường trung trực là nếu có nhiều đoạn thẳng song song, đường trung trực của chúng cũng là song song với các đoạn thẳng đó. Điều này có thể được chứng minh bằng cách sử dụng định lí song song.
Tổng hợp các tính chất trên, ta có thể tóm tắt tính chất chung của đường trung trực như sau: đường trung trực là đường thẳng duy nhất đi qua trung điểm của đoạn thẳng và vuông góc với đoạn thẳng đó. Đây là một đường quan trọng trong hình học và được sử dụng trong nhiều bài toán như xác định góc vuông, xác định điểm trung điểm và xác định đường thẳng song song.
Cảm ơn bạn đã xem bài viết Tính chất đường trung trực là gì? Tổng hợp đủ các tính chất tại thcshuynhphuoc-np.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Đường trung trực là đường chia đôi một đoạn thẳng.
2. Đường trung trực cắt đúng góc vuông với đoạn thẳng ban đầu.
3. Đường trung trực luôn đi qua trung điểm của đoạn thẳng.
4. Các đường trung trực của các đoạn thẳng cắt nhau tại một điểm duy nhất.
5. Đường trung trực hợp của hai đoạn thẳng song song là đường thẳng đi qua vô hạn điểm.
6. Đường trung trực của một tam giác là các đường trung trực của các cạnh tam giác đó.
7. Trong một tam giác đều, đường trung trực của mỗi cạnh cắt nhau tại một góc 120 độ.
8. Đường trung trực là một đường thẳng nối hai điểm chính giữa các cạnh của hình vuông.
9. Đường trung trực là đường chứa tất cả các điểm trong mặt phẳng có khoảng cách bằng nhau với hai đường thẳng ban đầu.
10. Đường trung trực có tính chất đối xứng so với đoạn thẳng ban đầu.
11. Một tam giác cân có đường trung trực đi qua đỉnh và trung điểm của đáy.
12. Trong một hình chữ nhật, các đường chéo là đường trung trực của lẻ các cạnh.
13. Đường trung trực có thể là một đường thẳng hoặc một đường cong tùy thuộc vào hình dạng của đoạn thẳng ban đầu.
14. Đường trung trực là đường nằm trên một mặt phẳng vuông góc với đoạn thẳng ban đầu.
15. Có thể xây dựng đường trung trực của một đoạn thẳng bằng công cụ vẽ đồ thị hoặc tin học đồ họa.


