Bạn đang xem bài viết Tính chất đường trung trực của một đoạn thẳng? Top 10 bài tập vận dụng tại thcshuynhphuoc-np.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Tính chất đường trung trực của một đoạn thẳng là một trong những kiến thức căn bản trong học hình học. Đường trung trực của một đoạn thẳng là một đường thẳng đi qua điểm giữa của đoạn thẳng và vuông góc với đoạn thẳng đó. Tính chất này đã được chứng minh và ứng dụng trong nhiều bài toán và vấn đề liên quan đến hình học phẳng.
Dưới đây là một số bài tập vận dụng tính chất đường trung trực:
1. Cho ABC là một tam giác vuông tại A và AD là đường trung trực của đoạn BC. Chứng minh rằng ADC cũng là tam giác vuông.
2. Cho AB là một đoạn thẳng, C là trung điểm của AB. Vẽ đường thẳng đi qua C và cắt AB tại D. Chứng minh rằng CD là đường trung trực của đoạn AB.
3. Cho ABCD là một hình bình hành, E là trung điểm của cạnh BC. Vẽ đường thẳng đi qua E và song song với AD, cắt CD tại F. Chứng minh rằng EF là đường trung trực của đoạn CD.
4. Cho ABCD là một hình chữ nhật có đường chéo AC. Gọi M là trung điểm của AC. Vẽ đường thẳng đi qua M và vuông góc với BD, cắt BD tại N. Chứng minh rằng MN là đường trung trực của đoạn BD.
5. Cho ABC là một tam giác. Đường trung trực của đoạn BC cắt đường trung trực của đoạn AC tại M. Chứng minh rằng điểm M là trung điểm của đoạn AB.
6. Cho ABC là một tam giác vuông tại A, BE là đường trung trực của đoạn AC. Chứng minh rằng AE^2 = AB x AC.
7. Cho ABCD là một hình tứ giác có AB // CD. Gọi E là giao điểm của AC và BD. Chứng minh rằng đường trung trực của đoạn AB và đường trung trực của đoạn CD cắt nhau tại E.
8. Cho ABCD là một hình tam giác vuông cân tại A, E là giao điểm của AB và CD. Chứng minh rằng đường trung trực của đoạn DE cắt AC tại gốc vuông.
9. Cho ABCD là một hình thang có AB // CD, E là trung điểm của AD. Vẽ đường thẳng đi qua E và vuông góc với BC, cắt BC tại F. Chứng minh rằng EF là đường trung trực của đoạn BC.
10. Cho ABCD là một hình tứ giác có AC // BD. Gọi M và N lần lượt là trung điểm của AB và CD. Chứng minh rằng đường trung trực của đoạn AD, BM và CN đồng quy.
Đường trung trực là gì? Tính chất đường trung trực của một đường thẳng là gì? Bài tập vận dụng trong bài tính chất đường trung trực của một đoạn thẳng. Chúng Tôi sẽ giải thích hết cho các bạn trong bài sau đây.
Tính chất đường trung trực của một đoạn thẳng
Đường trung trực là gì?
Đường trung trực là đường thẳng đi qua trung điểm của đoạn thẳng và vuông góc với đoạn thẳng gọi là đường trung trực của đoạn thẳng ấy.
Tính chất của đường trung trực:
- Tính chất đường trung trực của một đoạn thẳng
- Tính chất 3 đường trung trực trong tam giác.
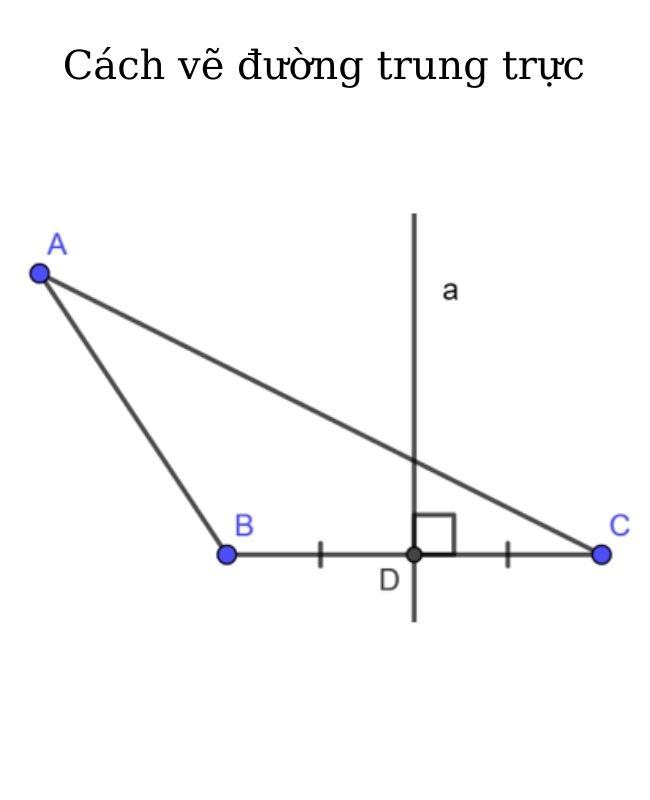
Cách vẽ đường trung trực của tam giác
Cách vẽ đường trung trực của một tam giác ABC cho trước:
- Vẽ tam giác ABC.
- Xác định trung điểm I của đoạn thẳng BC.
- Kẻ một đường thẳng a vuông góc với đoạn thẳng BC tại I.
- Ta có a là đường trung trực của tam giác ABC.
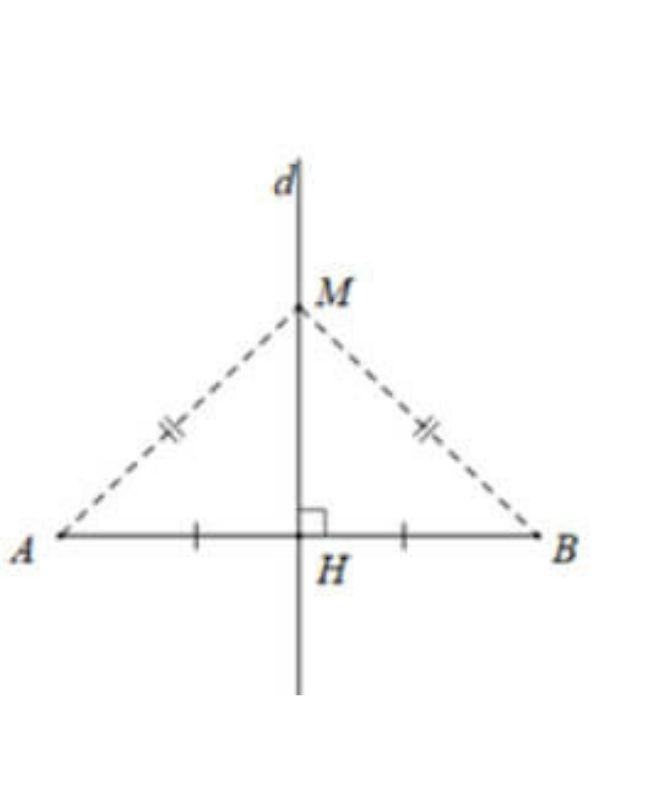
Định lí thuận
Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
GT: dd là trung trực của ABAB.
M∈dM∈d.
KL: MA=MB.
Định lí đảo
Điểm cách đều hai đầu mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.
Một số câu hỏi thường gặp
Số đường trung trực trong một đoạn thẳng?
Vì đường trung trực là đường thẳng đi qua trung điểm và vuông góc với đoạn thẳng. Mà mỗi đoạn thẳng chỉ có duy nhất một điểm là trung điểm cho nên mỗi đoạn thẳng có duy nhất 1 đường trung trực.
Cách viết phương trình đường trung trực của đoạn thẳng
Khi tìm hiểu về định nghĩa đường trung trực của đoạn thẳng, ta cũng cần biết cách viết phương trình đường trung trực của đoạn thẳng như sau:
Bước 1: Ta tìm vectơ pháp tuyến của đường trung trực và một điểm mà nó đi qua.
Bước 2: Ta dựa vào định lý 1: “Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó. Nghĩa là nếu điểm M thuộc đường thẳng AB thì thì MA = MB.
Ví dụ 1
Gọi M là điểm nằm trên đường trung trực của đoạn thẳng AB. Nếu MA có độ dài 5cm thì độ dài MB bằng bao nhiêu?
Giải: Vì điểm M nằm trên đường trung trực của đoạn thẳng AB nên theo định lí về tính chất của các điểm thuộc đường trung trực ta có MA = MB.
Mà MA = 5cm (gt) suy ra MB = 5cm.
Bài tập về tính chất đường trung trực của một đoạn thẳng
Sau đây Chúng Tôi sẽ đưa ra một số bài tập về tính chất đường trung trực của một đoạn thẳng
Bài 1
Cho tam giác ABC cân tại A. Hai trung tuyến BM, CN cắt nhau tại I. Hai tia phân giác trong của góc B và C cắt nhau tại O.Hai đường trung trực của 2 cạnh AB và AC cắt nhau tại K.
a) Chứng minh: BM = CN.
b) Chứng minh OB = OC.
c) Chứng minh các điểm A,O, I, K thẳng hàng.
Bài 2
Trên đường thẳng d là trung trực của đoạn thẳng AB lấy điểm M, N nằm ở hai nữa hai mặt phẳng đối nhau có bờ là đường thẳng AB.
a) Chứng minh.
b) MN là tia phân giác của AMB.
Bài 3
Cho góc xOy = 50, điểm A nằm trong góc xOy. Vẽ điểm M sao cho Ox là trung trực của đoạn AN, vẽ điểm M sao cho Oy là trung trực của đoạn AM.
a) Chứng minh: OM = ON.
b) Tính số đo.
Bài 4
Cho 2 điểm A và B nằm trên cùng một mặt phẳng có bờ là đường thẳng d. Vẽ điểm C sao cho d là trung trực của đường thẳng BC, AC cắt d tai E. Trên d lấy điểm M bất kỳ.
a) So sánh MA + MB và AC.
b) Tìm vị trí của M trên d để MA + MB ngắn nhất.
Bài 5
Cho tam giác ABC có góc A tù. Các đường trung trực của AB và AC cắt nhau tại O và cắt BC theo thứ tự ở D và E.
a) Các tam giác ABD, ACE là tam giác gì?
b) Đường tròn tâm O bán kinh OA đi qua những điểm nào trên hình vẽ?
Bài 6
Cho tam giác ABC vuông tại A ,đường cao AH. Vẽ đường trung trục của cạnh AC cắt BC tại I và cắt AC tại E.
a) Chứng minh IA = IB = IC.
b) Gọi M là trung điểm của đoạn AI, chứng minh MH = ME.
c) BE cắt AI tại N, tính tỉ số của đoạn MN và AI.
Bài 7
Cho 4 điểm A, B, C, D phân biệt. Với điều kiện nào sau đây thì đường thẳng AC là đường trung trực của đoạn thẳng BD?
Bài 8
Gọi M là điểm nằm trên đường trung trực của đoạn thẳng AB . Cho MA =5cm. Hỏi độ dài MB bằng?
Bài 9
Cho hai điểm M, N nằm trên đường trung trực của đoạn thẳng AB. Chứng minh ∆AMN = ∆BMN.
Bài 10
Cho ba tam giác ABC, DBC, EBC có chung đáy BC . Chứng minh 3 điểm A, D, E thẳng hàng.
Qua bài viết trên chắc hẳn các bạn đã hiểu được tính chất đường trung trực của một đoạn thẳng rồi nhỉ? Chúng Tôi đã giải thích rõ ràng ở bài viết trên, các bạn còn thắc mắc gì hãy để comment bên dưới nhé!
Kết Luận:
Tính chất đường trung trực của một đoạn thẳng là một thuộc tính quan trọng trong hình học. Nó giúp chúng ta hiểu rõ về mối quan hệ giữa các thành phần của một đoạn thẳng và các đường trung trực liên quan.
Một đường trung trực của một đoạn thẳng là một đường thẳng cắt đôi mảnh đối xứng của đoạn thẳng ở trung điểm của nó. Điều này đồng nghĩa với việc đường trung trực chia đôi đoạn thẳng thành hai phần bằng nhau về độ dài.
Đặc biệt, các đường trung trực cũng có một số tính chất đáng chú ý. Đầu tiên, tính chất đối xứng: mỗi điểm nằm trên đường trung trực đều có một điểm đối xứng qua đoạn thẳng ban đầu. Điều này có nghĩa là nếu ta lấy một điểm thuộc đoạn thẳng và kẻ một đoạn thẳng qua điểm đó và trung điểm của đoạn thẳng, thì đoạn thẳng này là đường trung trực của đoạn thẳng ban đầu.
Thứ hai, tính chất song song: mọi đường trung trực của một đoạn thẳng đều song song với nhau. Điều này có nghĩa là nếu ta có hai đoạn thẳng cùng chia đôi một đoạn thẳng bằng nhau, thì đường trung trực của chúng sẽ là những đường thẳng song song.
Cuối cùng, tính chất vận dụng: tính chất đường trung trực của một đoạn thẳng có thể được áp dụng trong nhiều bài tập và bài toán trong hình học. Ví dụ, tính chất đường trung trực có thể được sử dụng để tìm trung điểm của một đoạn thẳng, hay để chứng minh hai đoạn thẳng bằng nhau dựa trên tính chất đối xứng.
Trong tổng quát, tính chất đường trung trực của một đoạn thẳng là một khái niệm cơ bản trong hình học, mang lại kiến thức cơ bản và vận dụng trong nhiều bài tập và bài toán. Hiểu rõ về tính chất này giúp chúng ta phát triển khả năng suy luận và tư duy logic trong giải quyết các bài toán liên quan đến hình học.
Cảm ơn bạn đã xem bài viết Tính chất đường trung trực của một đoạn thẳng? Top 10 bài tập vận dụng tại thcshuynhphuoc-np.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Đường trung trực
2. Đoạn trung trực
3. Phương trình đường trung trực
4. Trung trực đoạn thẳng
5. Điểm trung trực
6. Giao điểm đường trung trực
7. Vị trí đối xứng
8. Đối xứng đường trung trực
9. Khoảng cách đến đường trung trực
10. Thang đo độ dài đường trung trực
11. Xác định đường trung trực qua hai điểm
12. Đường trung trực và đường vuông góc
13. Đoạn thẳng đối xứng
14. Vị trí tương đối giữa đoạn thẳng và đường trung trực
15. Bài tập vận dụng về tính chất đường trung trực


