Bạn đang xem bài viết Tính chất 2 tiếp tuyến cắt nhau – Bài tập sách giáo khoa Toán 9 tại thcshuynhphuoc-np.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Trong môn học Toán lớp 9, chúng ta sẽ tìm hiểu về tính chất 2 tiếp tuyến cắt nhau. Đây là một chủ đề quan trọng giúp chúng ta hiểu rõ hơn về các đường cong và quan hệ giữa chúng.
Tính chất 2 tiếp tuyến cắt nhau liên quan đến việc xác định điểm cắt của hai tiếp tuyến của hai đường cong. Điểm cắt này có vai trò quan trọng trong việc nghiên cứu tính chất và đặc điểm của hai đường cong đó.
Trong bài tập sách giáo khoa Toán 9, chúng ta sẽ được cung cấp nhiều ví dụ và bài tập thực hành để rèn luyện kỹ năng tìm điểm cắt của hai tiếp tuyến. Bằng cách làm các bài tập này, chúng ta sẽ hiểu rõ hơn về cách xác định và tính toán các điểm cắt đó.
Ngoài ra, tính chất 2 tiếp tuyến cắt nhau còn có ý nghĩa và ứng dụng trong nhiều lĩnh vực khác nhau của cuộc sống như ngành xây dựng, hoạt động của các hệ thống điều khiển tự động hay các bài toán tối ưu hóa. Việc nắm vững kiến thức về tính chất 2 tiếp tuyến cắt nhau sẽ giúp chúng ta ứng dụng linh hoạt và sáng tạo trong các bài toán thực tế.
Vậy, để hiểu rõ và áp dụng thành thạo tính chất 2 tiếp tuyến cắt nhau, hãy cùng nhau tìm hiểu và thực hành qua các bài tập sách giáo khoa Toán 9.
Tính chất 2 tiếp tuyến cắt nhau
Định lý về tính chất 2 tiếp tuyến cắt nhau
Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì:
- Điểm đó cách đều 2 tiếp điểm.
- Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.
- Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.
Nghĩa là cho đường tròn (O), B, C∈(O). Tiếp tuyến của (O) tại B,C cắt nhau tại A.

Khi đó
- AB=AC.
- Tia OC là phân giác góc BOC.
- Tia AO là phân giác góc BAC.
Chứng minh tính chất 2 tiếp tuyến cắt nhau
Muốn chứng minh tính chất 2 tiếp tuyến cắt nhau, trước tiên. Chúng ta hãy kẻ bảng giải thiết và kết luận để lắm rõ yêu cầu đề bài.
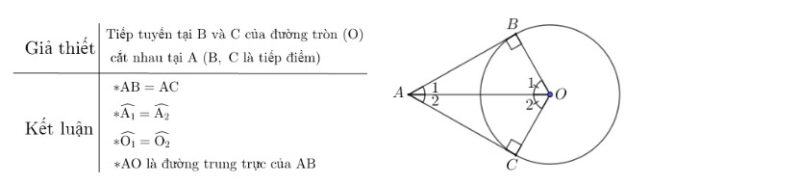
Gọi BA, CA theo thứ tự là các tiếp tuyến tại B và C của đường tròn (O). Theo tính chất 2 tiếp tuyến cắt nhau ta có:
AB vuông OB tại B và AC vuông OC tại C.
Xét tam giác OAB và tam giác OAC có:
- OB = OC
- Góc ABO = Góc ACO = 90
- AO là cạnh chung
Do đó, tam giác OAB = tam giác OAC (cạnh huyền – cạnh góc vuông)
Suy ra:
- Góc A1 =A2 (2 góc tương ứng)
- Góc O1= O2 (2 góc tương ứng)
- AB= AC suy ra A thuộc đường trung thực của đoạn BC
- Mà OB=OC suy ra O thuộc đường trung trực của đoạn BC
Kết luận OA là đường trung trực của đoạn BC
Đường tròn nội tiếp tam giác
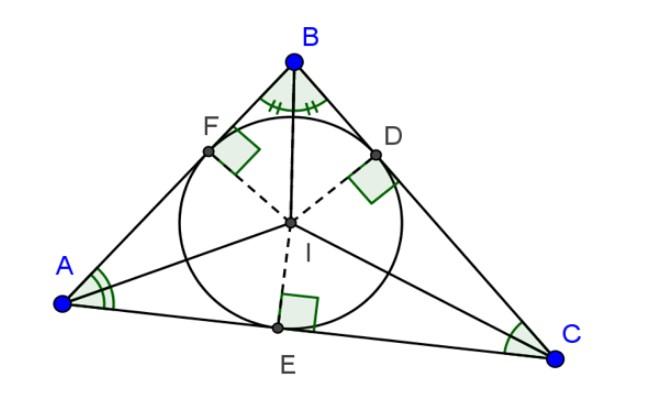
Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với ba cạnh của tam giác. Còn tam giác gọi là ngoại tiếp đường tròn. Tâm của đường tròn nội tiếp tam giác là giao điểm của các đường phân giác các góc trong của tam giác.
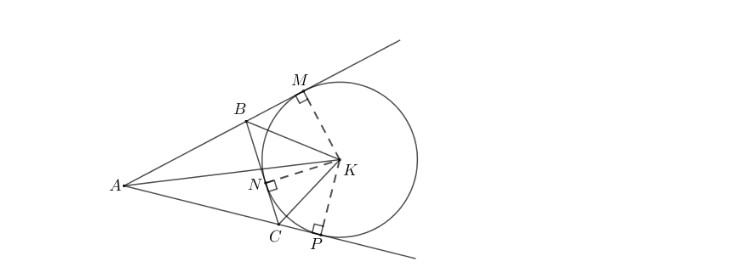
Đường tròn bàng tiếp tam giác
Đường tròn tiếp xúc với một cạnh của một tam giác và tiếp xúc với các phần kéo dài của hai cạnh kia gọi là đường tròn bàng tiếp tam giác.
Tâm của đường tròn bàng tiếp tam giác trong góc A là giao điểm của hai đường phân giác các góc ngoài tại B và C. Hoặc là giao điểm của đường phân giác góc A và đường phân giác góc ngoài tại B (hoặc C). Với một tam giác, có ba đường tròn bàng tiếp.
Các dạng bài toán thường gặp về tính chất 2 tiếp tuyến cắt nhau
Dạng 1: Chứng minh các đường thẳng song song (vuông góc), chứng minh hai đoạn thẳng bằng nhau.
Phương pháp: Dùng tính chất của hai tiếp tuyến cắt nhau.
Dạng 2: Chứng minh một đường thẳng là tiếp tuyến, tính độ dài, số đo góc và các yếu tố khác.
Phương pháp:
- Dùng định nghĩa tiếp tuyến; tính chất của hai tiếp tuyến cắt nhau.
- Dùng khái niệm đường tròn nội tiếp, bàng tiếp.
- Dùng hệ thức lượng về cạnh và góc trong tam giác vuông.
Bài tập liên quan đến tính chất 2 tiếp tuyến cắt nhau
Sau khi ôn lại kiến thức về định nghĩa và tính chất 2 tiếp tuyến cắt nhau. Thì cùng Chúng Tôi củng cố lại kiến thức qua một số bài tập minh hoạ về tính chất 2 tiếp tuyến cắt nhau ngay nhé!
Giải bài 26 trang 115 – SGK Toán lớp 9 tập 1
Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm).
a) Chứng minh rằng OA vuông góc với BC.
b) Vẽ đường kính CD. Chứng minh rằng BD song song với AO.
c) Tính độ dài các cạnh của tam giác ABC; biết OB=2cm, OA=4cm.
Lời giải:
a) Ta có: AB = AC (tính chất 2 tiếp tuyến cắt nhau). Nên ΔABC cân tại A.
Lại có AO là tia phân giác của góc A nên AO ⊥ BC. (Trong tam giác cân, đường phân giác cũng là đường cao)
b) Gọi I là giao điểm của AO và BC. Suy ra BI = IC (đường kính vuông góc với một dây).
Xét ΔCBD có:
CI = IB
CO = OD (bán kính)
⇒ BD // HO (HO là đường trung bình của BCD) ⇒ BD // AO.
c) Theo định lí Pitago trong tam giác vuông OAC:

Giải bài 27 trang 115 – SGK Toán lớp 9 tập 1
Từ một điểm A nằm bên ngoài đường tròn (O), kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Qua điểm M thuộc cung nhỏ BC, kẻ tiếp tuyến với đường tròn (O), nó cắt các tiếp tuyến AB và AC theo thứ tự ở D và E. Chứng minh rằng chu vi tam giác ADE bằng 2AB.
Lời giải:
Theo tính chất 2 tiếp tuyến cắt nhau ta có:
DM = DB, EM = EC, AB = AC
Chu vi ΔADE:
Chu vi ΔADE = AD + DE + AE = AD + DM + ME + AE = AD + DB + EC + AE = AB + AC = 2AB (đpcm)
Giải bài 28 trang 116 – SGK Toán lớp 9 tập 1
Cho góc xAy khác góc bẹt. Tâm của các đường tròn tiếp xúc với hai cạnh của góc xAy nằm trên đường nào?
Lời giải:
Gọi O là tâm của một đường tròn bất kì tiếp xúc với hai cạnh góc xAy. Theo tính chất của hai tiếp tuyến cắt nhau ta có: góc xOA = góc yOA.
Hay AO là tia phân giác của góc xAy.
Vậy tâm các đường tròn tiếp xúc với hai cạnh của góc xAy nằm trên tia phân giác của góc xAy.
Giải bài 29 trang 116 – SGK Toán lớp 9 tập 1
Cho góc xAy khác góc bẹt, điểm B thuộc tia Ax. Hãy dựng đường tròn (O) tiếp xúc với Ax tại B và tiếp xúc với Ay.
Lời giải:
Đường tròn (O) tiếp xúc với hai tia Ax và Ay nên tâm O của (O) nằm trên tia phân giác của góc xAy. Do đó ta có cách dựng:
- Dựng tia phân giác At của góc xAy.
- Dựng đường thẳng Bz qua B và vuông góc với tia Ax.
- Giao điểm O của At và Bz là tâm của đường tròn cần dựng.
- Dựng đường tròn tâm O, bán kính R = OB, ta được đường tròn cần dựng.

Hy vọng bài viết giúp các bạn hiểu được tính chất 2 tiếp tuyến cắt nhau và một số bài tập SGK Toán 9. Đừng quên share và follow bài viết để Chúng Tôi có thêm động lực chia sẻ kiến thức nữa nhé.
Trong bài tập sách giáo khoa Toán 9, chúng ta được học về tính chất 2 tiếp tuyến cắt nhau của đường tròn và đường thẳng. Tính chất này rất quan trọng và có nhiều ứng dụng trong thực tế.
Tính chất 2 tiếp tuyến cắt nhau giúp ta xác định tọa độ các điểm cắt của đường tròn và đường thẳng. Khi một đường tròn và một đường thẳng cắt nhau một điểm, đường thẳng đó được gọi là tiếp tuyến của đường tròn tại điểm cắt này. Nếu một đường thẳng cắt đường tròn tại 2 điểm, ta có 2 tiếp tuyến cắt nhau.
Việc hiểu và áp dụng tính chất này giúp chúng ta giải quyết các bài toán về hình học trong thực tế. Ví dụ, trong công nghệ, khi thiết kế các vật thể tròn, ta cần biết đường thẳng nào là tiếp tuyến của đường tròn, để có thể vẽ một mặt phẳng vuông góc với đường thẳng đó, ổn định vị trí vật thể tròn. Ngoài ra, kiến thức về tính chất này cũng có thể được áp dụng trong lĩnh vực địa hình, quy hoạch đô thị và nhiều ngành công nghiệp khác.
Tính chất 2 tiếp tuyến cắt nhau cũng giúp ta hiểu rõ hơn về hình ảnh của đường tròn và đường thẳng. Điều này giúp ta nhận biết các tình huống đặc biệt, như đường thẳng đi qua tâm của đường tròn, khiến chúng trở thành tiếp tuyến duy nhất. Việc nhận biết và hiểu rõ về các tình huống này giúp ta phát hiện ra các quy luật và tính chất mới của hình học, và từ đó mở rộng tri thức của mình.
Tóm lại, việc hiểu và áp dụng tính chất 2 tiếp tuyến cắt nhau trong bài tập sách giáo khoa Toán 9 là rất cần thiết. Tính chất này không chỉ giúp ta giải quyết các bài toán hình học, mà còn có nhiều ứng dụng thực tế. Việc áp dụng tính chất này không chỉ giúp chúng ta hiểu rõ hơn về hình ảnh của đường tròn và đường thẳng, mà còn giúp ta phát hiện ra những quy luật và tính chất mới trong hình học.
Cảm ơn bạn đã xem bài viết Tính chất 2 tiếp tuyến cắt nhau – Bài tập sách giáo khoa Toán 9 tại thcshuynhphuoc-np.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Tiếp tuyến
2. Cắt nhau
3. Đường tròn
4. Đường thẳng
5. Hình học Euclid
6. Giao điểm
7. Phép cắt
8. Góc cắt
9. Giao nhau
10. Điểm chung
11. Cạnh chung
12. Mặt phẳng chung
13. Đường chéo
14. Cách biệt
15. Góc tù


