Bạn đang xem bài viết Thể tích khối lăng trụ tam giác đều? Bài tập vận dụng tại thcshuynhphuoc-np.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Trong học tập toán học, chúng ta thường gặp phải các bài tập liên quan đến tính toán thể tích của các hình học khác nhau. Trong bài viết này, chúng ta sẽ tìm hiểu về thể tích của khối lăng trụ tam giác đều, một dạng hình học rất phổ biến và thú vị.
Một khối lăng trụ tam giác đều là một hình hộp có hai đáy là hai tam giác đều cân, và các cạnh bên là các đoạn thẳng nối các đỉnh tương ứng của hai tam giác đó. Đặc biệt, tất cả các cạnh bên của khối lăng trụ tam giác đều có cùng chiều dài. Để tính toán thể tích của khối lăng trụ tam giác đều, ta cần biết các kích thước của tam giác và chiều dài cạnh bên khối lăng trụ.
Bài tập vận dụng đòi hỏi chúng ta áp dụng nguyên lý và công thức tính thể tích vào thực tế. Ví dụ, chúng ta có thể được cho biết chiều cao của khối lăng trụ tam giác đều, hoặc lựa chọn một số giá trị cho chiều dài cạnh bên và các thông số của tam giác. Sau đó, ta sẽ sử dụng các công thức tính thể tích để tính toán kết quả.
Qua việc giải quyết bài tập vận dụng này, chúng ta không chỉ rèn luyện kỹ năng tính toán mà còn áp dụng kiến thức toán học vào thực tiễn. Mở rộng hiểu biết của chúng ta về hình học không gian và rèn luyện tư duy logic.
Thể tích khối lăng trụ tam giác đều là một phần kiến thức phổ biến và quan trọng trong Toán hình học không gian. Hãy tham khảo bài viết sau đây của Chúng Tôi để hiểu rõ hơn về phần kiến thức này nhé!
Hình lăng trụ tam giác đều là gì?
Hình lăng trụ là gì?
Hình lăng trụ trong toán hình học không gian được định nghĩa là một khối đa diện bao gồm hai đáy. Hai đáy là hai đa giác bằng nhau và nằm trên hai mặt phẳng song song.
Ngoài ra, các mặt bên của hình lăng trụ là hình bình hành. Các cạnh bên trong hình lăng trụ sẽ song song hoặc bằng nhau.
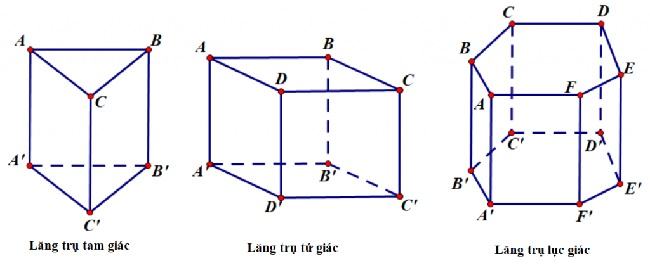
Hình lăng trụ tam giác đều là gì?
Hình lăng trụ tam giác đều là hình lăng trụ có hai đáy là hai tam giác đều. Lăng trụ tam giác đều sẽ có 4 mặt đối xứng với nhau.
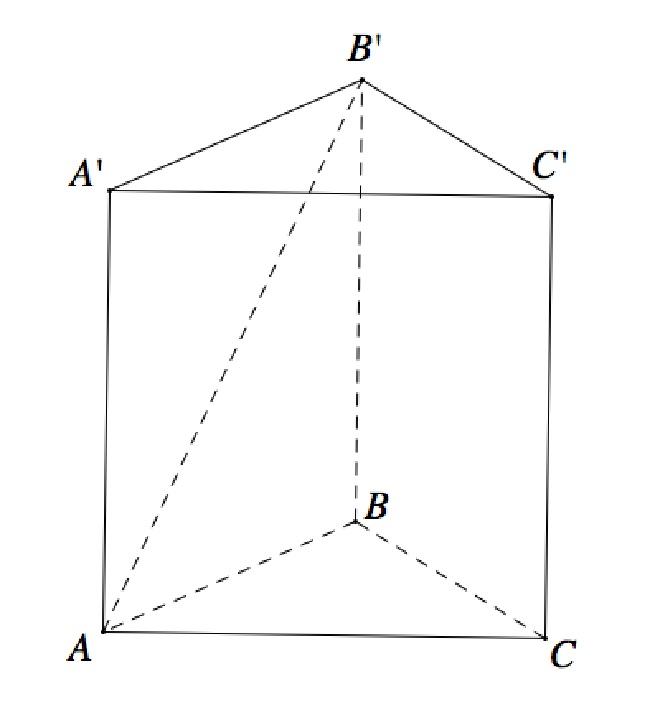
Tính chất hình lăng trụ tam giác đều
Hình lăng trụ tam giác đều có 3 tính chất cơ bản sau:
- Lăng trụ tam giác đều có các cạnh bên vuông góc với mặt đáy.
- Lăng trụ tam giác đều có các mặt bên là hình chữ nhật.
- Lăng trụ tam giác đều có hai đáy là hai tam giác đều bằng nhau. Do đó, các cạnh đáy sẽ bằng nhau.
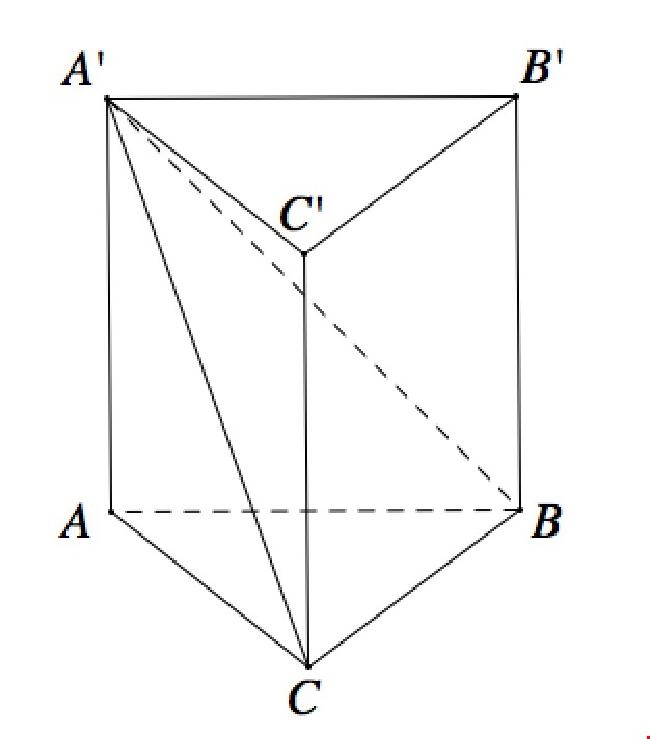
Dấu hiệu nhận biết hình lăng trụ tam giác đều
Chúng ta có thể nhận biết hình lăng trụ tam giác đều bằng cách nhìn vào hai đáy của hình lăng trụ đứng. Nếu hai đáy là hai tam giác đều thì đó chính là hình lăng trụ tam giác đều.
Xem thêm:
- Tính chất trọng tâm tam giác và cách xác định trọng tâm
- Các trường hợp đồng dạng của tam giác vuông cần nhớ
- Tính chất ba đường cao của tam giác và bài tập áp dụng
Thể tích khối lăng trụ tam giác đều
Công thức tính thể tích khối lăng trụ tam giác đều
Thể tích khối hình lăng trụ tam giác đều sẽ bằng diện tích của mặt đáy và khoảng cách giữa hai mặt đáy hoặc là chiều cao.
Từ đó chúng ta có công thức tính thể tích hình lăng trụ tam giác giác đều như sau:
V = B.h
Trong đó:
- V là thể tích khối lăng trụ tam giác đều( đơn vị m3).
- B là diện tích khối lăng trụ tam giác đều ( đơn vị m2).
- h là chiều cao khối lăng trụ tam giác đều( đơn vị m).
Diện tích của mặt đáy tam giác đều của khối lăng trụ tam giác đều được tính dựa trên công thức:
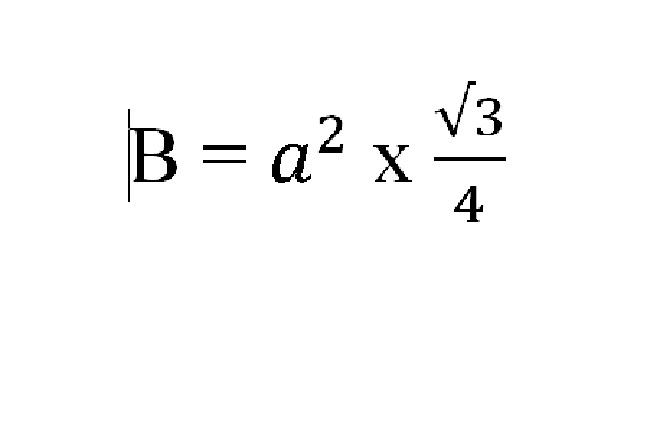
Ví dụ cho tính thể tích khối lăng trụ tam giác đều.
Một bể nước hình trụ có diện tích mặt đáy B = 2 m2 và đường cao h = 1 m. Thể tích của bể nước này bằng bao nhiêu?
Trả lời:
Áp dụng công thức tính thể tích khối lăng trụ tam giác đều ta có:
V = B.h = 2.1 = 2 m3.
Tiếp theo hãy cùng Chúng Tôi đi đến phần bài tập để hiểu rõ hơn về công thức tính thể tích khối lăng trụ tam giác đều nhé!
Bài tập vận dụng
Bài tập 1: Tính thể tích khối trụ tam giác đều ABCA’B’C’ có độ dài cạnh đáy bằng 8cm và mặt phẳng A’B’C’ tạo với mặt đáy ABC một góc bằng 60 độ.
Trả lời:
Gọi I là trung điểm của đoạn thẳng BC ta có:
AI vuông góc BC (theo tính chất đường trung tuyến của một tam giác đều)
A’I vuông góc BC (Vì A’BC là tam giác cân)
Góc A’BC, ABC = góc AIA’ = 60 độ
![]()
Diện tích tam giác ABC là:
![]()
Thể tích khối lăng trụ tam giác đều ABCA’B’C’ là:
![]()
Bài tập 2. Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh bằng a = 2 cm và chiều cao là h = 3cm. Hãy tính thể tích hình lăng trụ này?
Trả lời:
Vì đáy là tam giác đều cạnh a nên diện tích:
![]()
Vậy thể tích khối lăng trụ là:
![]()
Bài tập 3: Tính thể tích của khối lăng trụ tam giác đều có cạnh đáy bằng 2a và cạnh bên bằng a?
Trả lời:

Bài tập 4:
Cho hình lăng trụ tam giác đều ABC.A’B’C’. Hãy tính thể tích khối lăng trụ này
a) AB = 2 cm; AA’ = 6 cm
b) AB = 6 cm; BB’ = 8 cm
c) BC = 3,5 cm; CC’ = 6 cm
Trả lời:
a) Theo đề
a = AB = 2 cm; h = AA’ = 6 cm
Áp dụng công thức tính thể tích lăng trụ tam giác đều ta có:
![]()
b) Theo đề
a = AB = 6 cm; h = BB’ = 8 cm
Áp dụng công thức tính thể tích khối lăng trụ tam giác đều ta có:
![]()
c) Theo đề:
a = BC = 3,5 cm; h = CC’ = 6 cm
Áp dụng công thức tính thể tích lăng trụ tam giác đều ta có:
![]()
Trên đây là toàn bộ kiến thức liên quan đến công thức tính thể tích khối lăng trụ tam giác đều. Hy vọng bài viết này của Chúng Tôi đã giải đáp được những thắc mắc của các bạn. Hãy theo dõi Chúng Tôi mỗi ngày để biết thêm nhiều thông tin hay và bổ ích nhé!
Qua bài viết trên, ta đã tìm hiểu về định nghĩa và cách tính thể tích của khối lăng trụ tam giác đều. Đầu tiên, chúng ta cần biết khái niệm về khối lăng trụ tam giác đều, đó là một hình hộp có hình dạng của một tam giác đều, với tất cả các cạnh của tam giác đều song song với mặt đáy của hình hộp.
Để tính thể tích của khối lăng trụ tam giác đều, ta sử dụng công thức:
V = A * h,
trong đó V là thể tích của khối lăng trụ tam giác đều, A là diện tích đáy của khối lăng trụ, và h là chiều cao của khối lăng trụ.
Qua ví dụ và bài tập vận dụng, chúng ta đã thấy cách áp dụng công thức trên vào việc tính toán thể tích của khối lăng trụ tam giác đều trong các tình huống khác nhau. Việc tìm hiểu và áp dụng công thức này giúp chúng ta hiểu rõ hơn về tính chất của hình học và khả năng tính toán trong đó.
Bên cạnh đó, việc vận dụng kiến thức về thể tích khối lăng trụ tam giác đều góp phần trong việc giải quyết các bài toán liên quan đến thiết kế và xây dựng trong đời sống hàng ngày. Chẳng hạn, khi tính toán thể tích những khối lăng trụ tam giác đều như hộp đựng, bồn chứa, nút giao thông, ta có thể đảm bảo tính chính xác và đáng tin cậy cho công việc.
Tuy nhiên, việc thực hiện các tính toán thể tích này đòi hỏi chúng ta phải biết cách làm việc với đơn vị đo lường, làm quen với phép tính toán và có kiến thức vững chắc về hình học. Nắm vững kiến thức và kỹ năng này sẽ giúp chúng ta thành công trong việc vận dụng thể tích khối lăng trụ tam giác đều trong thực tế.
Tóm lại, việc nắm vững kiến thức về thể tích khối lăng trụ tam giác đều giúp chúng ta không chỉ hiểu rõ tính chất của hình học mà còn có khả năng áp dụng vào việc giải quyết bài toán và tăng cường sự chính xác trong công việc. Để thành công trong việc này, chúng ta cần áp dụng công thức tính thể tích và có kiến thức vững chắc về hình học.
Cảm ơn bạn đã xem bài viết Thể tích khối lăng trụ tam giác đều? Bài tập vận dụng tại thcshuynhphuoc-np.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Thể tích lăng trụ tam giác đều
2. Thể tích khối lăng trụ tam giác đều
3. Vận dụng thể tích lăng trụ tam giác đều
4. Bài tập vận dụng thể tích lăng trụ tam giác đều
5. Công thức tính thể tích lăng trụ tam giác đều
6. Ví dụ về thể tích lăng trụ tam giác đều
7. Bài tập thực hành về thể tích lăng trụ tam giác đều
8. Tính thể tích lăng trụ tam giác đều
9. Bài tập căn bản về thể tích lăng trụ tam giác đều
10. Tính thể tích lăng trụ có tam giác đều là đáy
11. Công thức tính diện tích xung quanh của lăng trụ tam giác đều
12. Tính thể tích và diện tích xung quanh của lăng trụ tam giác đều
13. Thể tích lăng trụ tứ diện đều
14. Bài tập vận dụng tính diện tích xung quanh lăng trụ tam giác đều
15. Công thức tính thể tích của lăng trụ hình tam giác đều


