Bạn đang xem bài viết Sự xác định đường tròn – tính chất đối xứng của đường tròn tại thcshuynhphuoc-np.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Đường tròn là một trong những hình học cơ bản và quan trọng trong toán học. Được xác định bằng cách lấy tập hợp tất cả các điểm thuộc mặt phẳng cách một điểm đã cho (tâm) một khoảng cách không đổi (bán kính). Sự xác định đường tròn không chỉ đơn giản là một định nghĩa hình học, mà còn được chứng minh thông qua nhiều tính chất quan trọng như tính chất đối xứng.
Tính chất đối xứng của đường tròn là một khía cạnh quan trọng trong việc nghiên cứu hình học của nó. Đường tròn có tính chất đối xứng theo mọi điểm trên đường kính. Điều này có nghĩa là nếu chúng ta chọn một điểm bất kỳ nằm trên đường tròn làm tâm và vẽ đường kính đi qua điểm đó, thì các đoạn thẳng từ tâm đến các điểm trên đường kính này đều có cùng một độ dài.
Tính chất đối xứng của đường tròn không chỉ áp dụng cho đường kính mà còn cho mọi đoạn thẳng nằm trong đường tròn. Điều này có nghĩa là nếu chúng ta chọn hai điểm bất kỳ trên đường tròn và vẽ một đoạn thẳng nối hai điểm đó, thì đoạn thẳng này sẽ chia đường tròn thành hai phần có diện tích bằng nhau. Đây chính là tính chất đối xứng trong hình học của đường tròn.
Sự xác định đường tròn và tính chất đối xứng của nó có vai trò quan trọng trong nhiều lĩnh vực như hình học, vật lý đại cương, hoặc ứng dụng trong công nghệ thông tin. Hiểu rõ và áp dụng một cách chính xác các tính chất này có thể giúp chúng ta giải quyết các vấn đề toán học phức tạp và xây dựng các ứng dụng hiệu quả trong thực tế.
Sự xác định đường tròn – tính chất đối xứng của đường tròn là bài học quan trọng trong chương trình lớp 9. Cùng Chúng Tôi tổng hợp lại kiến thức nhé!
Sự xác định đường tròn – tính chất đối xứng của đường tròn
Bài viết dưới đây sẽ cung cấp cho bạn kiến thức, định nghĩa và cách làm bài tập về sự xác định đường tròn – tính chất đối xứng của đường tròn. Đầu tiên, hãy cùng Chúng Tôi tìm hiểu khái niệm về đường tròn ngay thôi nào.
Định nghĩa đường tròn
Đường tròn là tập hợp của tất cả những điểm trên một mặt phẳng, cách đều một điểm cho trước bằng một khoảng cách nào đó.
Điểm cho trước gọi là tâm của đường tròn, còn khoảng cho trước gọi là bán kính của đường tròn. Đường tròn tâm O bán kính R ký hiệu là (O;R).
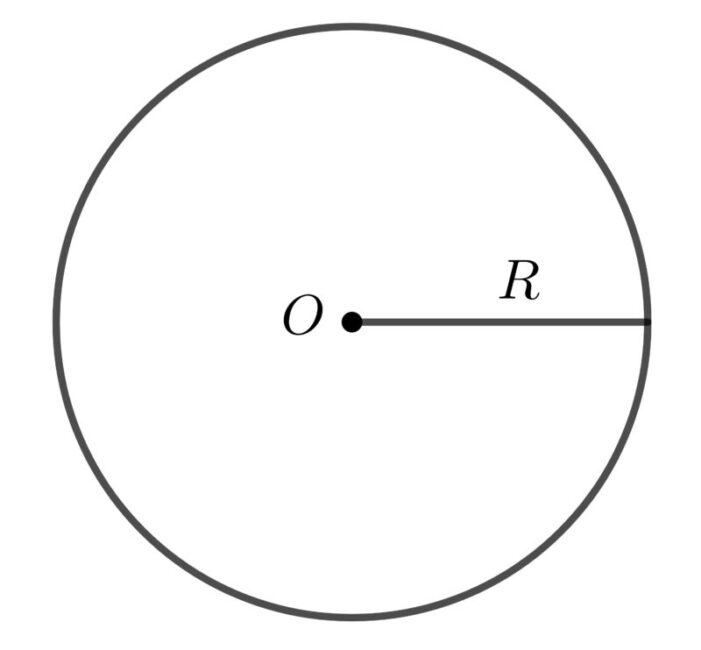
Ngoài ra, đường tròn còn được định nghĩa là một hình khép kín đơn giản chia mặt phẳng ra làm 2 phần. Hai phần đó là phần bên trong và phần bên ngoài.
Định lý về sự xác định một đường tròn
Có hai định lý về sự xác định một đường tròn. Cụ thể như sau:
Định lý 1: Qua ba điểm không thẳng hàng ta vẽ được một và chỉ một đường tròn.
Định lý 2: Đường tròn đi qua ba đỉnh của một tam giác gọi là đường tròn ngoại tiếp tam giác. Tâm đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của tam giác đó.
Tính chất đối xứng của đường tròn
Về tính chất đối xứng thì đường tròn là hình vừa có tâm đối xứng, vừa có trục đối xứng. Mỗi tính chất sẽ có một đặc điểm riêng. Cụ thể như sau:
Tính chất 1: Tâm đối xứng
Đường tròn là hình có tâm đối xứng. Tâm của đường tròn là tâm đối xứng của đường tròn đó.
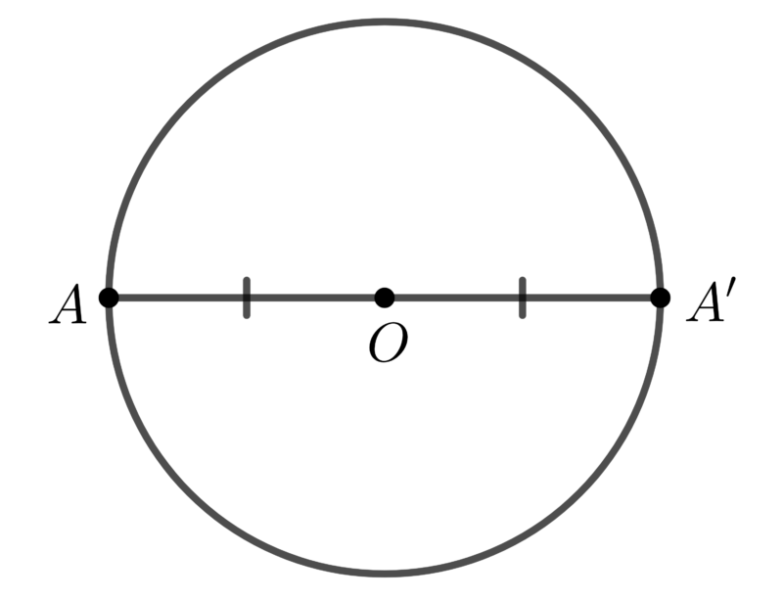
Tính chất 2: Trục đối xứng
Đường tròn là hình có trục đối xứng. Bất kì đường kính nào cũng là trục đối xứng của đường tròn.
Lưu ý: Trong tam giác vuông trung điểm cạnh huyền là tâm đường tròn ngoại tiếp.
Trong tam giác đều, tâm đường tròn ngoại tiếp là trọng tâm tam giác đó.
Bài tập về sự xác định đường tròn – tính chất đối xứng của đường tròn
Có 3 dạng bài cơ bản về sự xác định đường tròn – tính chất đối xứng của đường tròn. Cùng theo dõi từng dạng bài cụ thể với Chúng Tôi nhé!
Dạng 1: Chứng minh các điểm cho trước cùng thuộc một đường tròn
Phương pháp: Chứng minh các điểm cho trước cùng cách đều một điểm nào đó. Điểm đó chính là tâm của đường tròn.
Bài tập 1: Cho tam giác ABC vuông tại A, đường cao AH. Từ M là điểm bất kì trên cạnh BC kẻ MD ⊥ AB, ME ⊥ AC. Chứng minh 5 điểm A, D, M, H, E cùng nằm trên một đường tròn.
Hướng dẫn:
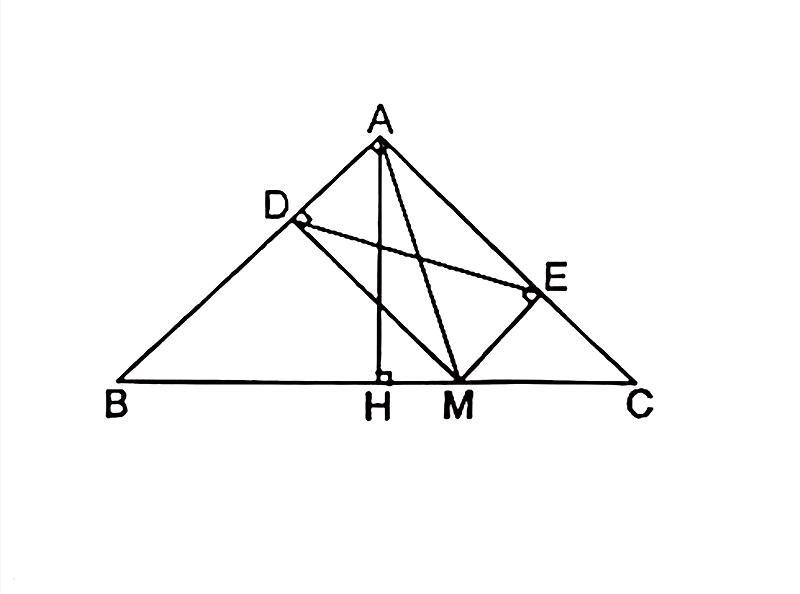
Vì ba tam giác vuông ADM, AEM, AHM có chung cạnh huyền AM nên 3 đỉnh góc vuông nằm trên đường tròn đường kính AM có tâm là trung điểm của AM.
Vây 5 điểm A, D, H, E cùng nằm trên một đường tròn.
Tham khảo thêm kiến thức:
- Tính chất đường phân giác trong tam giác?
- Tính chất hình thang vuông?
Dạng 2: Xác định vị trí tương đối của một điểm đối với một đường tròn
Phương pháp: Để xác định vị trí của điểm M đối với đường tròn (O;R) ta so sánh khoảng cách OM với bán kính R
- Nếu A nằm trên đường tròn (O;R) thì OA = R
- Nếu A nằm trong đường tròn (O;R) thì OA < R
- Nếu A nằm ngoài đường tròn (O;R) thì OA >R
Bài tập 2: Cho đường tròn (O), AB là một đường kính bất kỳ và C là một điểm thuộc đường tròn. Vẽ C’ đối xứng với điểm C qua AB. Chứng minh rằng điểm C’ cũng thuộc đường tròn (O).
Hướng dẫn:
Do C và C’ đối xứng nhau qua AB nên AB là đường trung trực của CC’
⇒ O nằm trên đường trung trực của CC’
⇒ OC = OC’ = R
⇒ C’ cũng thuộc đường tròn (O)
Dạng 3: Xác định tâm và tính bán kính đường tròn ngoại tiếp
Phương pháp: Ta thường sử dụng các kiến thức sau:
- Sử dụng tính chất đường trung tuyến trong tam giác vuông.
- Dùng định lý Pytago.
- Dùng hệ thức lượng về cạnh và góc trong tam giác vuông.
Bài tập 3: Cho tam giác ABC vuông tại A, và AB = 6cm, BC = 8cm. Xác định bán kính đường tròn ngoại tiếp tam giác ABC bằng bao nhiêu?
Hướng dẫn:
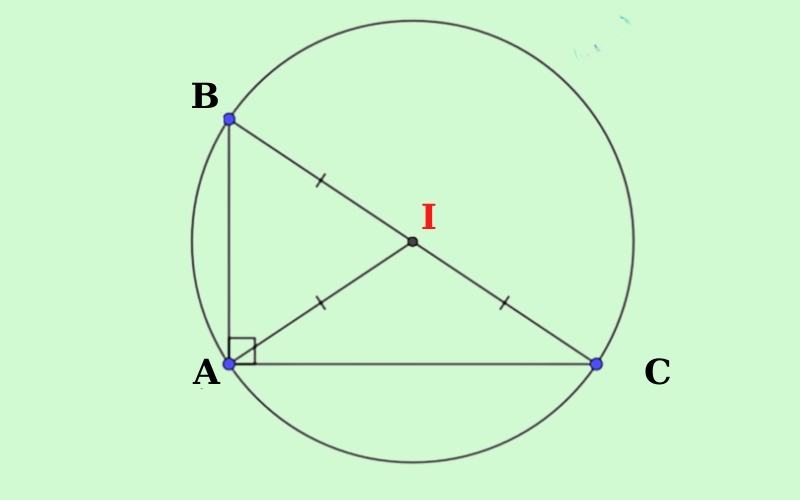
Áp dụng định lý Pytago ta có:
BC^2 = AB^2 + BC ^2 => BC = 10 cm.
Ta lại có: ∆ABC vuông tại A có AI là đường trung tuyến ứng với cạnh huyền BC. I là tâm đường tròn ngoại tiếp ∆ABC.
=> CI = 1/2 BC
=> IA = IB = IC = 5cm
Vậy đường tròn ngoại tiếp ∆ABC có bán kính đường tròn ngoại tiếp là R = IC = 5 cm.
Vậy là chúng ta đã tìm hiểu xong bài sự xác định đường tròn – tính chất đối xứng của đường tròn. Ngoài định nghĩa, tính chất của đường tròn, Chúng Tôi còn cung cấp thêm một vài dạng bài minh họa để bạn dễ hình dung hơn. Hãy theo dõi chúng tôi để có nhiều bài học bổ ích hơn nhé!
Trong bài viết này, chúng ta đã tìm hiểu về sự xác định đường tròn và tính chất đối xứng của đường tròn.
Đầu tiên, chúng ta đã hiểu rõ cách xác định đường tròn bằng cách biết tâm và bán kính của nó. Bằng cách sử dụng công thức định nghĩa, chúng ta có thể tính được các thông số khác nhau của đường tròn như chu vi, diện tích và tọa độ các điểm trên đường tròn.
Ngoài ra, chúng ta cũng đã tìm hiểu về tính chất đối xứng của đường tròn. Đường tròn có nhiều loại đối xứng như đối xứng qua trục tung, đối xứng qua trục hoành và đối xứng qua gốc tọa độ. Nhờ tính chất đối xứng này, chúng ta có thể dễ dàng tìm các điểm đối xứng trên đường tròn và xác định nhanh chóng các đường tròn đồng trục hoặc tương đồng.
Đường tròn là một khái niệm quan trọng trong hình học và được ứng dụng rộng rãi trong thực tế. Chúng ta có thể thấy các đường tròn trong các ứng dụng hàng ngày như vòng đo kích thước, đồ họa máy tính, thiết kế mạch điện và nhiều lĩnh vực khác.
Từ việc hiểu rõ sự xác định đường tròn và tính chất đối xứng của nó, chúng ta có thể áp dụng kiến thức này vào việc giải quyết các bài toán và vận dụng vào thế giới thực. Sự hiểu biết này không chỉ giúp chúng ta mở rộng kiến thức về hình học mà còn hỗ trợ trong việc phát triển tư duy logic và khả năng vận dụng.
Cảm ơn bạn đã xem bài viết Sự xác định đường tròn – tính chất đối xứng của đường tròn tại thcshuynhphuoc-np.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Đường tròn
2. Tâm đường tròn
3. Bán kính đường tròn
4. Đường kính đường tròn
5. Đường tròn tâm O
6. Điểm thuộc đường tròn
7. Giao điểm đường tròn
8. Phân tâm đường tròn
9. Phân tía đường tròn
10. Đường tròn đồng tâm
11. Đường tròn đồng quy
12. Tính chất đối xứng của đường tròn
13. Trục đồng tâm
14. Phương trình đường tròn
15. Tính chất đường tròn tiếp xúc với đường thẳng.


