Bạn đang xem bài viết Hàm số nghịch biến khi nào? Lý thuyết và bài tập tại thcshuynhphuoc-np.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Hàm số nghịch biến là một khái niệm quan trọng trong toán học, đặc biệt là trong môn học đại số và giải tích. Hàm số nghịch biến được xác định dựa trên sự thay đổi của giá trị hàm khi biến độc lập thay đổi. Trong bài viết này, chúng ta sẽ tìm hiểu về lý thuyết và thực hành về hàm số nghịch biến.
Để hiểu được khái niệm hàm số nghịch biến, ta cần phân biệt hai khái niệm chính là tăng và giảm. Một hàm số được gọi là tăng trên một khoảng nếu giá trị hàm tăng khi giá trị biến độc lập tăng. Ngược lại, nếu giá trị hàm giảm khi giá trị biến độc lập tăng, hàm số được gọi là giảm trên khoảng đó.
Trong trường hợp hàm số đảo ngược sự tăng và giảm của một hàm số, chúng ta có thể nói rằng hàm số đó là hàm số nghịch biến. Tức là, khi giá trị biến độc lập tăng, giá trị hàm giảm và ngược lại, khi giá trị biến độc lập giảm, giá trị hàm tăng.
Để xác định một hàm số nghịch biến, ta thường sử dụng phương pháp kiểm tra đạo hàm. Nếu đạo hàm của hàm số là âm trên một khoảng, tức là hàm số giảm trên khoảng đó. Ngược lại, nếu đạo hàm của hàm số là dương trên một khoảng, hàm số tăng trên khoảng đó.
Bên cạnh lý thuyết, chúng ta cũng cần thực hành để làm quen với kiểm tra tính nghịch biến của một hàm số. Vì vậy, trong bài viết này, chúng ta cũng sẽ giải một số bài tập về hàm số nghịch biến. Điều này giúp bạn có thể áp dụng kiến thức nhận được vào thực tế và cải thiện kỹ năng giải toán của mình.
Qua bài viết này, hy vọng bạn sẽ hiểu rõ hơn về khái niệm hàm số nghịch biến và có thể áp dụng kiến thức đã học vào việc giải quyết các bài toán thực tế. Ngoài ra, hãy không ngần ngại hỏi và thảo luận để tiếp tục làm rõ các khái niệm khó khăn hơn và nâng cao hiểu biết của mình về hàm số nghịch biến.
Dạng toán hàm số nghịch biến thường xuất hiện nhiều trong các đề thi THPTQG và trong các đề thi thử của các trường trên toàn quốc. Nhiều bạn vẫn thắc mắc Hàm số nghịch biến khi nào? Điều kiện của nó là gì? Bài viết này của Chúng Tôi sẽ giải đáp và giúp các bạn ôn tập tốt dạng toán này!
Định nghĩa hàm số nghịch biến
Hàm số nghịch biến, đồng biến hay còn gọi là hàm số đơn điệu.
Cho K là một khoảng, một đoạn hoặc một nửa khoảng và y = f(x) là một hàm số xác định trên K.
Hàm số y = f(x) được gọi là nghịch biến (giảm) trên K, nếu:
- ∀ x1, x2 ∊ K mà x1 < x2 thì f (x1) > f (x2)
- Biểu diễn đồ thị hàm số là một đường đi xuống.
Hàm số nghịch biến khi nào?
Hàm số f nghịch biến trên K khi và chỉ khi:
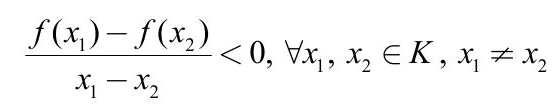
Điều kiện đủ để hàm số nghịch biến
Cho hàm số f có đạo hàm trên K.
Nếu f'(x) < 0 với mọi x ∈ K thì f nghịch biến trên K.
Định lí mở rộng
Chỉ xét K là một khoảng
Giả sử hàm số f có đạo hàm trên K
Nếu f'(x) ≤ 0 với mọi x ∈ K và f'(x) = 0 chỉ tại một số hữu hạn điểm thuộc K thì f nghịch biến trên K.
Phương pháp xét tính đơn điệu của hàm số
- Tìm tập xác định
- Tính đạo hàm f'(x). Tìm các điểm xi (i= 1 , 2 ,…, n) mà tại đó f'(x) bằng 0 hoặc không xác định.
- Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên.
- Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.
Bài tập mẫu
Dạng toán xét sự đồng biến, nghịch biến của hàm số

Kết luận: Hàm số đồng biến trên các khoảng (-∞;2) và (4;+∞), nghịch biến trên khoảng (2;4).

Dạng toán tìm m để hàm số nghịch biến
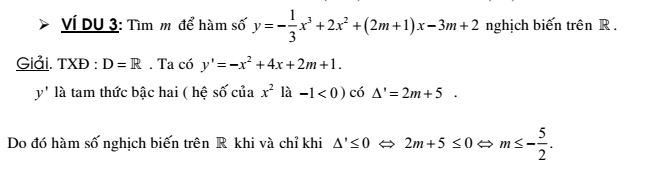
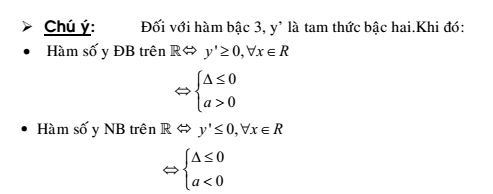
Ví dụ 4: Tìm m để hàm số: ![]() nghịch biến trong khoảng (-1/2;1/2)
nghịch biến trong khoảng (-1/2;1/2)

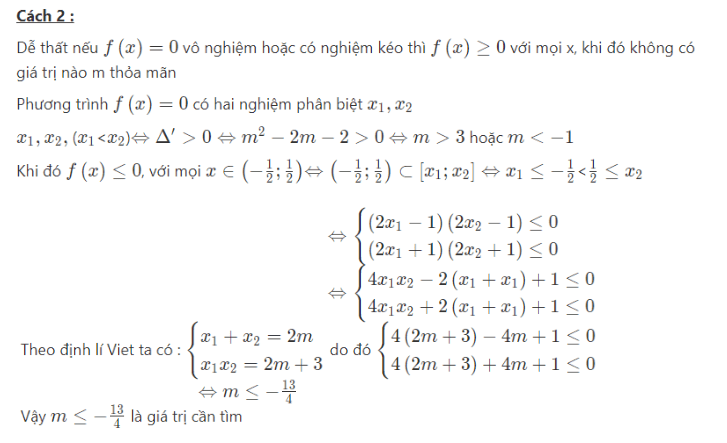
Qua những kiến thức trên mà Chúng Tôi chia sẻ, hy vọng bạn đọc sẽ nắm vững kiến thức về hàm số nghịch biến khi nào và ôn tập thật tốt. Chúc các bạn thành công!
Trong chủ đề “Hàm số nghịch biến khi nào?”, chúng ta đã học về khái niệm của hàm số nghịch biến và tìm hiểu cách xác định khi nào một hàm số mang tính chất này. Chúng ta cũng đã làm quen với lý thuyết và áp dụng bài tập để phát triển khả năng hiểu và áp dụng các nguyên tắc cơ bản liên quan đến hàm số nghịch biến.
Ban đầu, chúng ta đã định nghĩa hàm số nghịch biến là loại hàm mà khi tăng một biến số thì hàm đó giảm và ngược lại, khi giảm biến số thì hàm tăng. Điều này có thể được mô tả bằng các giá trị của đạo hàm. Với hàm số nghịch biến, đạo hàm của nó luôn đối diện một chiều với biến số. Nghĩa là, khi đạo hàm là dương, hàm giảm và khi đạo hàm là âm, hàm tăng.
Để xác định khi nào một hàm số nghịch biến, chúng ta có thể áp dụng một số quy tắc và phương pháp. Đầu tiên, chúng ta có thể tìm đạo hàm của hàm số. Sau đó, chúng ta sẽ xác định dấu của đạo hàm và từ đó xác định xem hàm tăng hay giảm. Nếu đạo hàm là dương, hàm giảm và ngược lại, nếu đạo hàm là âm, hàm tăng. Dựa trên thông tin này, chúng ta có thể kết luận được khi nào hàm số nghịch biến.
Ngoài ra, trong quá trình học tập, chúng ta đã có cơ hội áp dụng kiến thức này qua các bài tập. Trong các bài tập này, chúng ta đã được yêu cầu xác định xem một hàm số có nghịch biến hay không, và tìm giá trị của biến số khi hàm số đạt cực trị. Chúng ta đã sử dụng các phương pháp tính toán và phân tích để giải quyết các bài tập này, từ đó rèn luyện kỹ năng về hàm số nghịch biến.
Tổng kết lại, chủ đề “Hàm số nghịch biến khi nào?” đã cung cấp cho chúng ta kiến thức và phương pháp để xác định, hiểu và áp dụng các tính chất của hàm số nghịch biến. Chúng ta đã học lý thuyết và từ đó áp dụng vào tìm giải các bài tập. Qua quá trình này, chúng ta đã phát triển khả năng dùng logic và tính toán để xác định tính chất của hàm số và ứng dụng vào các bài toán thực tế.
Cảm ơn bạn đã xem bài viết Hàm số nghịch biến khi nào? Lý thuyết và bài tập tại thcshuynhphuoc-np.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Hàm số nghịch biến là gì?
2. Định nghĩa hàm số nghịch biến.
3. Điều kiện để hàm số nghịch biến.
4. Đặc trưng của đồ thị hàm số nghịch biến.
5. Hàm số biến đổi nghịch biến qua phép dời, co giãn và đối xứng.
6. Ví dụ minh họa về hàm số nghịch biến.
7. Cách xác định hàm số có nghịch biến hay không.
8. Tính chất quan trọng của hàm số nghịch biến.
9. Công thức tính đạo hàm của hàm số nghịch biến.
10. Cách vẽ đồ thị hàm số nghịch biến.
11. Bài tập về hàm số nghịch biến.
12. Ví dụ về phản ví dụ của hàm số nghịch biến.
13. Biểu đồ hàm số nghịch biến.
14. Quy tắc nhân và chia trong hàm số nghịch biến.
15. Ứng dụng của hàm số nghịch biến trong thực tế.


