Bạn đang xem bài viết Đường cao trong tam giác cân là gì? Bài tập cách tính nhanh (kèm đáp án) tại thcshuynhphuoc-np.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Trong lĩnh vực hình học, tam giác là một dạng hình học cơ bản được nghiên cứu và áp dụng rộng rãi. Trong tam giác, đường cao là một khái niệm quan trọng và điều tiên quyết để giải các bài toán liên quan đến tỷ lệ và hình học của tam giác.
Tam giác cân là một dạng đặc biệt của tam giác, trong đó hai cạnh đối xứng với nhau qua đường trung tuyến và gốc của tam giác cùng nằm trên một đường cao. Đặc điểm này giúp tam giác cân có một số thuộc tính và tính chất độc đáo.
Một trong những tính chất quan trọng của tam giác cân là đường cao cũng là đường trung tuyến và phân chia tam giác thành hai tam giác đều, có cùng cạnh đáy và góc ở đỉnh. Điều này khiến cho việc tính toán và xác định các đặc tính của tam giác cân trở nên dễ dàng hơn.
Để tính nhanh đường cao trong tam giác cân, chúng ta có thể áp dụng các công thức và quy tắc hình học đã được phát triển từ trước. Một trong những công thức phổ biến là công thức tính chiều cao của tam giác cân.
Công thức tính nhanh chiều cao trong tam giác cân là:
Đường cao = căn bậc hai của 2 * cạnh đáy * căn bậc hai của 1 trừ đi căn bậc hai của 0.5.
Ví dụ, hãy tính nhanh đường cao trong tam giác cân ABC, với AB là cạnh đáy có độ dài 8 đơn vị.
Sử dụng công thức, ta có:
Đường cao = căn bậc hai của 2 * 8 * căn bậc hai của 1 trừ đi căn bậc hai của 0.5
= căn bậc hai của 16 * căn bậc hai của 1 – căn bậc hai của 0.5
= căn bậc hai của 16 * 1 – căn bậc hai của 0.5
= căn bậc hai của 16 – căn bậc hai của 0.5
≈ 4 – 0.71
≈ 3.29.
Vậy đường cao trong tam giác cân ABC, với AB là cạnh đáy có độ dài 8 đơn vị, có độ dài tương đương khoảng 3.29 đơn vị.
Từ công thức trên, chúng ta có thể áp dụng vào các bài toán thực tế và tính toán nhanh chóng đường cao trong tam giác cân.
Bên cạnh các công thức tính diện tích, tính chu vi tam giác thì cách tính đường cao trong tam giác cân cũng là một trong những dạng bài tập thường gặp ở Toán lớp 9. Vậy đường cao trong tam giác cân là gì? Cùng Chúng Tôi tìm hiểu qua bài viết sau đây.
Đường cao trong tam giác là gì?
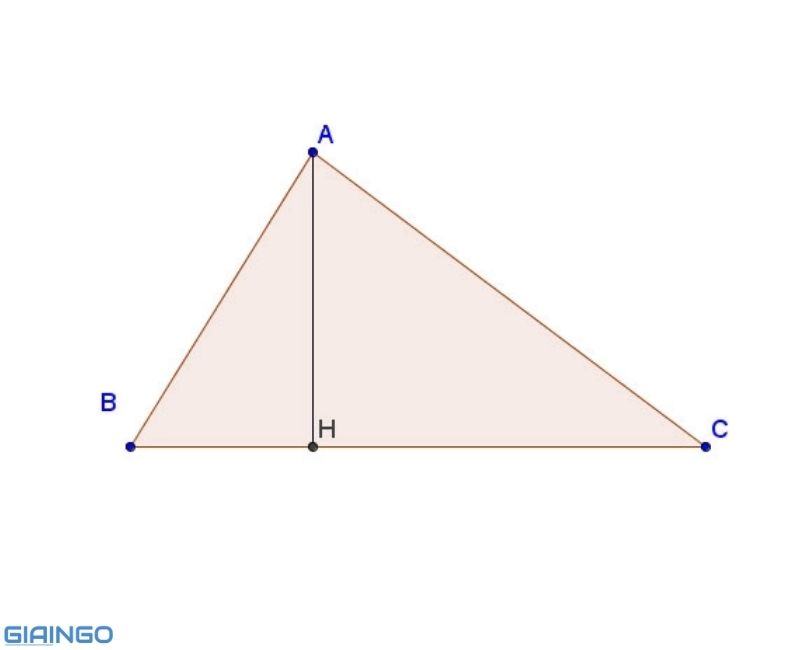
Đường cao trong tam giác là đoạn thẳng kẻ từ một đỉnh và vuông góc với cạnh đối diện. Cạnh đối diện này được gọi là đáy tương ứng với đường cao.
Mỗi tam giác có 3 đường cao. Độ dài của đường cao trong tam giác được xác định là khoảng cách giữa đỉnh và đáy.
Khi làm bài tập, các bạn cần phải xác định đúng và phân loại được các loại đường cao trong tam giác thường, vuông, cân để giải cho nhanh và chính xác.
Từ đường cao trong tam giác, bạn dễ dàng suy luận đường cao trong tam giác cân là gì rồi nhé!
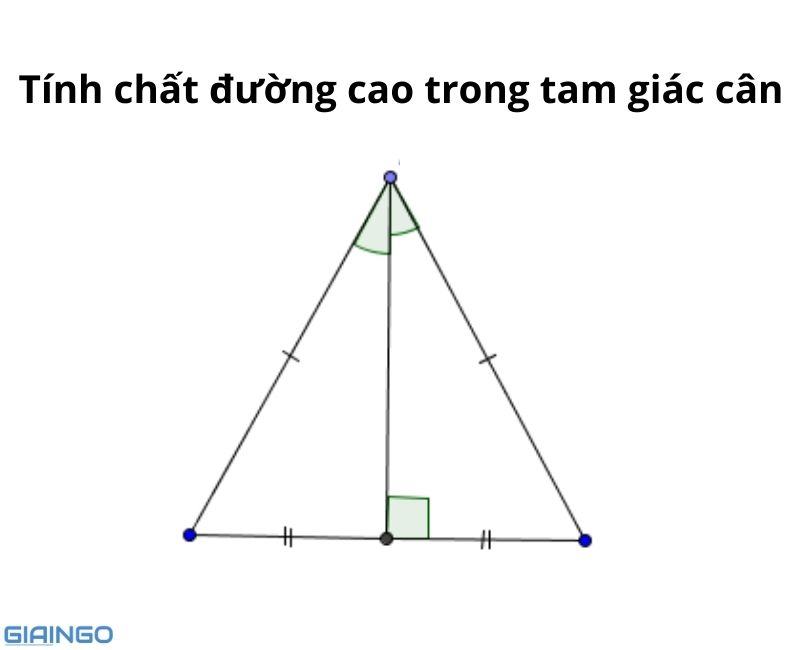
Tính chất đường cao trong tam giác cân
Tính chất đường cao trong tam giác cân gồm:
- Đường cao tam giác cân đi qua trung điểm của cạnh đáy tương ứng.
- Đường cao tam giác cân đồng thời cũng là đường phân giác của góc ở đỉnh và đường trung trực của đáy tương ứng.
- Nếu như một tam giác các có đường cao đồng thời cũng là đường trung tuyến hoặc phân giác thì tam giác đó chính là tam giác cân.
Công thức tính đường cao trong tam giác cân
Đường cao trong tam giác cân bằng bình phương độ dài một cạnh của tam giác trừ bình phương độ dài cạnh đáy chia bốn.
Công thức: h2 = a2 − b2/4
Trong đó:
- h: Chiều cao của tam giác cân
- a: Cạnh của tam giác cân
- b: Cạnh đáy tương ứng với chiều cao từ đỉnh của hình tam giác cân
Như vậy, khi biết thành phần như độ dài một cạnh của tam giác và cạnh đáy tương ứng với chiều cao từ đỉnh của là có thể tính được đường cao trong tam giác.
Ví dụ: Cho tam giác ABC cân tại A, đường cao AH vuông góc tại H như sau. Tính đường cao AH.
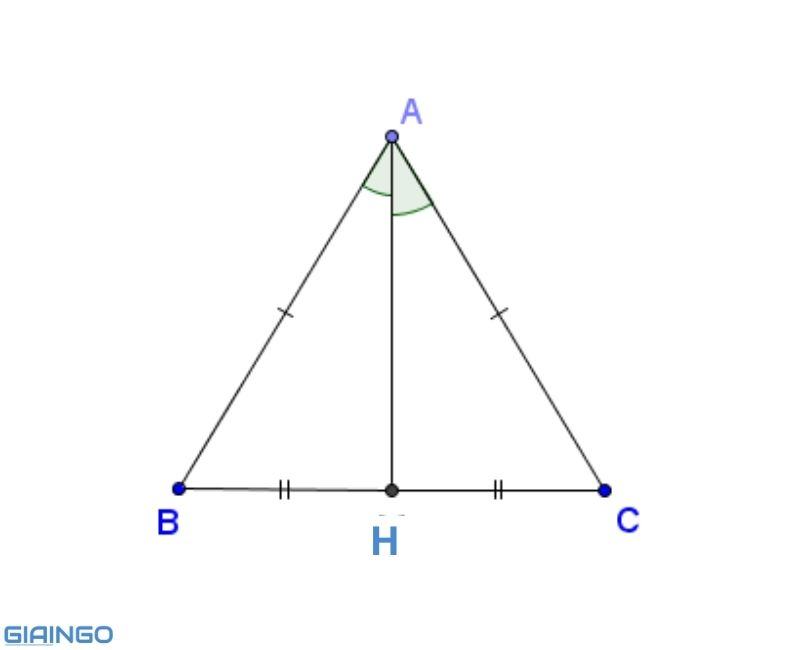
Hướng dẫn
Vì tam giác ABC cân tại A, đường cao AH đồng thời là đường trung tuyến nên:
Áp dụng định lý Pythagore trong tam giác vuông ABH vuông tại H ta có:
AH2 + BH2 = AB2
=> AH2 = AB2 − BH2
Cách tính đường cao trong tam giác cân thật đơn giản phải đúng không nào. Hãy ghi chú cẩn thận và tùy từng trường hợp mà áp dụng cho chính xác nhé.
Xem thêm:
- Tính chất đường phân giác trong tam giác? Lý thuyết & bài tập
- Cách chứng minh tam giác cân? Dấu hiệu, tính chất, công thức
- Tính chất trọng tâm tam giác và cách xác định trọng tâm
Bài tập về tính đường cao trong tam giác cân
Để hiểu hơn về nội dung đường cao trong tam giác cân, chúng ta cùng giải các bài tập về tính đường cao trong tam giác cân nhé.
Bài tập 1
Cho tam giác cân ABC cân tại A có độ dài hai cạnh AB = AC = 4cm, BC = 14m. Tính chiều dài đường cao trong tam giác cân ABC.
Trả lời
Kẻ đường cao AH vuông góc với BC tại H.
Vì đường cao tam giác cân đi qua trung điểm của cạnh đáy nên:
BH = HC = BC/2 = 14/2 = 7 cm
Áp dụng công thức bên trên ta có:
AH2 + BH2 = AB2
=> AH2 = AB2 − BH2 = 16 – 7 = 9
Độ dài AH = √9 = 3 cm.
Bài tập 2
Tính chiều dài đường cao trong tam giác cân có độ dài 2 cạnh bằng nhau là 2cm và độ dài cạnh còn lại là 3.
Trả lời
Áp dụng công thức trên ta có :
Độ dài đường cao trong tam giác cân h = √[ a2 – (b/2)2] = √(4 – (1.5)2) = 1.32 (cm)
Bài tập 3
Cho tam giác DEF cân tại A có DE + DF = 22cm, EF = 10. Kẻ DI vuông góc với EF tại I. Tính độ dài đường cao DI.
Trả lời
Vì tam giác DEF cân tại D nên DE = DF = 22/2 = 11 cm
Vì đường cao tam giác cân đi qua trung điểm của cạnh đáy nên
EI = IF = EF/2 = 10/2 = 5 cm
Áp dụng công thức bên trên ta có:
DI2 + EI2 = DE2
=> DI2 = DE2 − EI2 = 121 – 25 = 96
Độ dài DI = √96 = 4√6 cm.
Bài tập 4
Cho tam giác MNP, 2 đường cao MH và NE cắt nhau tại G. Chọn đáp án đúng:
A. G là trọng tâm của tam giác MNP.
B. G là tâm đường tròn nội tiếp tam giác MNP.
C. PG là đường cao của tam giác MNP.
D. PG là đường trung trực của tam giác MNP.
Đáp án: B
Bài tập 5
Cho tam giác MNP cân tại M biết MH là đường trung tuyến khi đó:
A. MHNP vuông góc.
B. MH là đường trung trực của NP.
C. MH là đường phân giác của góc NMP.
D. A, B, C đều đúng.
Đáp án: D

Vừa rồi Chúng Tôi đã chia sẻ cho bạn những thông tin về đường cao trong tam giác cân. Hy vọng qua bài viết trên bạn đã làm được chính xác dạng Toán này. Đừng quên theo dõi Chúng Tôi để biết thêm nhiều kiến thức bổ ích trong học tập nhé!
Cách tính đường cao trong tam giác cân thật đơn giản phải đúng không nào. Hãy ghi chú cẩn thận và tùy từng trường hợp mà áp dụng cho chính xác nhé.
Tổng kết lại, đường cao trong tam giác cân là đoạn thẳng kết nối đỉnh của tam giác với đáy và vuông góc với đáy. Trên đường cao này, ta có thể áp dụng công thức tính diện tích tam giác nhanh chóng và dễ dàng. Để tính diện tích của một tam giác cân, ta có thể sử dụng công thức: Diện tích = (cạnh đáy * chiều cao) / 2. Đáp án cho bài tập cách tính nhanh là diện tích tam giác cân được tính bằng cách nhân cạnh đáy với chiều cao và chia đôi.
Cảm ơn bạn đã xem bài viết Đường cao trong tam giác cân là gì? Bài tập cách tính nhanh (kèm đáp án) tại thcshuynhphuoc-np.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Định nghĩa đường cao trong tam giác cân
2. Công thức tính đường cao trong tam giác cân
3. Cách tính nhanh đường cao trong tam giác cân
4. Đường cao trong tam giác cân hình thành như thế nào?
5. Đường cao trong tam giác cân và tính chất tương đương
6. Đường cao trong tam giác cân chia đôi cạnh đáy như thế nào?
7. Tính đường cao trong tam giác cân khi biết đỉnh và đáy
8. Bài tập tính đường cao trong tam giác cân
9. Đường cao trong tam giác cân là gì?
10. Vẽ đường cao trong tam giác cân
11. Đường cao trong tam giác cân và góc nhọn
12. Vẽ đường cao trong tam giác cân dựa vào góc vuông
13. Bài tập tính toán đường cao trong tam giác cân
14. Đường cao trong tam giác cân và tính chất của tam giác cân
15. Đường cao trong tam giác cân và ứng dụng trong thực tế


