Bạn đang xem bài viết Định lý Talet trong tam giác và những hệ quả của định lý tại thcshuynhphuoc-np.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Trong lĩnh vực học tam giác, định lý Talet là một trong những định lý quan trọng và mang tính ứng dụng cao. Định lý này được đặt theo tên của nhà toán học người Hy Lạp, Tha-lês, người đã đưa ra định lý này vào khoảng thế kỷ thứ VI TCN.
Định lý Talet xác định quan hệ giữa độ dài 3 cạnh của một tam giác vuông. Theo đó, độ dài bình phương của cạnh huyền của tam giác vuông bằng tổng độ dài bình phương hai cạnh góc vuông còn lại. Đây là một công thức toán học cơ bản, nhưng lại có ứng dụng rất rộng trong nhiều lĩnh vực như hình học, vật lý, xây dựng…
Từ định lý Talet, ta có thể tìm ra các tính chất và hệ quả quan trọng khác trong tam giác. Một trong số đó là điều kiện tồn tại tam giác vuông, khi mà tổng bình phương hai cạnh nhỏ hơn bình phương cạnh lớn nhất. Bên cạnh đó, định lý Talet cũng được sử dụng trong việc tính toán các đại lượng trong tam giác như diện tích, chu vi, các góc tam giác mà không cần phải biết giá trị chính xác của các cạnh.
Ngoài ra, định lý Talet còn giúp chúng ta hiểu rõ hơn về tỷ lệ giữa các cạnh trong tam giác vuông. Khi biết một cạnh, ta có thể tính toán được cả hai cạnh còn lại dựa trên định lý này. Điều này rất hữu ích trong thực tế khi ta cần tính toán các kích thước, cân đối trong xây dựng, thiết kế hoặc các ứng dụng khác.
Tổng kết lại, định lý Talet là một công thức toán học quan trọng và có ảnh hưởng sâu sắc đối với nhiều lĩnh vực. Không chỉ giúp chúng ta hiểu và tính toán các thuộc tính của tam giác vuông mà còn mang lại những ứng dụng rộng rãi trong thực tế.
Định lý Talet trong tam giác là một trong những định lý được sử dụng nhiều nhất trong toán học. Với định lý này, ta có thể chứng minh nhiều hệ thức trong hình học và ứng dụng vào tính toán thực tế. Cùng Chúng Tôi tìm hiểu chi tiết nhé!
Định lý Talet trong tam giác
Định lý Talet trong tam giác hay còn được gọi là định lý Thales là một định lý có vai trò rất quan trọng trong lĩnh vực hình học nói riêng và trong Toán học nói chung.
Định lý này được đặt theo tên của một nhà Toán học đến từ Hy Lạp là Thales.
Định lý thuận
Định lí Talet trong tam giác được phát biểu rằng khi có 1 đường thẳng song song với 1 cạnh của tam giác. Đồng thời cắt 2 cạnh còn lại thì sẽ định ra trên 2 cạnh được cắt đó những đoạn thẳng có tỷ lệ tương ứng nhau.
Cho tam giác ABC như hình vẽ, BC // B’C’ thì:

Định lý đảo
Định lý Talet trong tam giác là một định lý mang tính chất 2 chiều, đó là chiều thuận và chiều đảo ngược.
Định lý Talet đảo được phát biểu như sau: Nếu trong một tam giác, một đường thẳng cắt 2 cạnh của tam giác đó và định ra trên 2 cạnh được cắt những đoạn thẳng tương ứng tỉ lệ với nhau thì đường thẳng đó sẽ song song với cạnh còn lại.
Cho tam giác ABC như hình vẽ, nếu ta có:
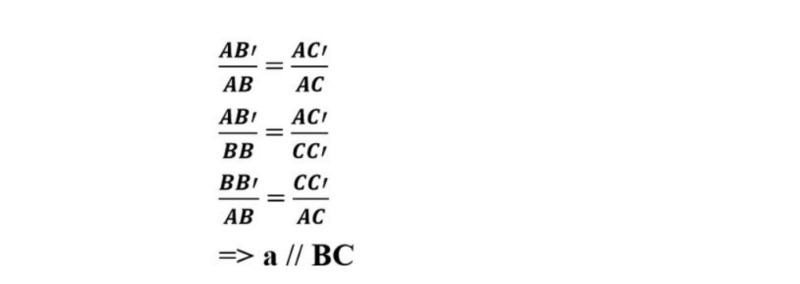
Chú ý: Hệ quả trên vẫn đúng cho trường hợp đường thẳng a song song với một cạnh của tam giác và cắt phần kéo dài của hai cạnh còn lại.
Những hệ quả của định lý Talet trong tam giác
Hệ quả 1
Một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì sẽ tạo ra một tam giác mới có 3 cạnh tỉ lệ với 3 cạnh của tam giác ban đầu.
Hệ quả 2
Một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì sẽ tạo ra một tam giác mới đồng dạng với tam giác ban đầu.
Hệ quả 3
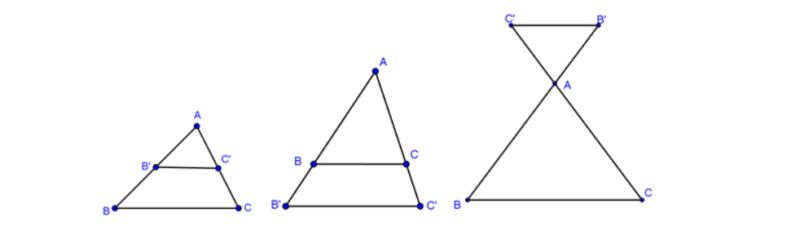
Hệ quả 3 – Talet mở rộng: Ba đường thẳng đồng quy thì chắn trên hai đường thẳng song song các cặp đoạn thẳng tỉ lệ.
Xem thêm:
- Đường cao trong tam giác cân là gì? Tính chất, công thức, cách tính
- Trực tâm là gì? 3 cách xác định trực tâm trong tam giác
- Tâm đường tròn ngoại tiếp tam giác là gì? Bài tập vận dụng
Bài tập minh họa định lý Talet trong tam giác SGK lớp 8
Trả lời câu hỏi Toán 8 Tập 2 Bài 1 trang 56
Cho AB = 3cm; CD = 5cm; AB/CD=?, EF = 4dm; MN = 7dm; EF/MN= ?
Lời giải:
AB/CD= 3/5
EF/MN= 4/7
Trả lời câu hỏi Toán 8 Tập 2 Bài 1 trang 57
Cho bốn đoạn thẳng AB, CD, A’B’, C’D’. So sánh tỉ số
Lời giải:
AB/CD= 2/3, A’B’/C’D’=4/6=2/3
Vậy AB/CD = A’B’/C’D’
Trả lời câu hỏi Toán 8 Tập 2 Bài 1 trang 57
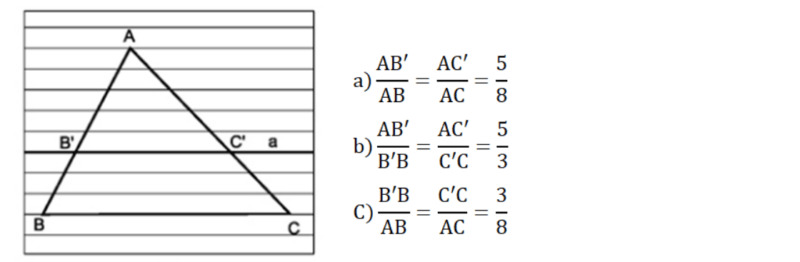
Vẽ tam giác ABC trên giấy kẻ học sinh như trên hình 3. Dựng đường thẳng a song song với cạnh BC, cắt hai cạnh AB, AC theo thứ tự tại B’ và C’.
Đường thẳng a định ra trên cạnh AB ba đoạn thẳng AB’, B’B và AB, và định ra trên cạnh AC ba đoạn thẳng tương ứng là AC’, C’C và AC. So sánh các tỉ số:
Lời giải:
Bài 1 (trang 58 SGK Toán 8 tập 2)
Viết tỉ số của hai đoạn thẳng có độ dài như sau:
Lời giải:
a) Ta có AB = 5cm và CD = 15 cm
AB/ CD= 5/15=1/3
b) EF= 48 cm, GH = 16 dm = 160 cm
EF/GH=48/160= 3/10
c) PQ= 1,2m = 120cm, MN= 24cm
PQ/MN=120/24=5
Bài 2 (trang 59 SGK Toán 8 tập 2)
Cho biết AB/CD=3/4 và CD bằng 12cm. Tính độ dài của AB.
Lời giải:
Ta có: AB/CD=3/4 mà CD= 12cm nên AB=(12×3)/4=9cm
Vậy AB= 9cm.
Bài 3 (trang 59 SGK Toán 8 tập 2)
Cho biết độ dài của AB gấp 5 lần độ dài của CD và độ dài của A’B’ gấp 12 lần độ dài của CD. Tính tỉ số của hai đoạn thẳng AB và A’B’.
Lời giải:
Độ dài AB gấp 5 lần độ dài của CD nên AB = 5CD.
Độ dài A’B’ gấp 12 lần độ dài của CD nên A’B’ = 12CD.
⇒ Tỉ số của hai đoạn thẳng AB và A’B’ là:
AB/A’B’= 5CD/12CD=5/12
Bài 4 (trang 59 SGK Toán 8 tập 2)

Bài 5 (trang 59 SGK Toán 8 tập 2)
Tính x trong các trường hợp sau
a) Ta có: MN // BC
Áp dụng định lý Talet trong tam giác ta có: AM/MB= AN/NC
Mà AM = 4, AN = 5, NC = AC – AN = 8,5 – 5 = 3,5
Suy ra: 4/x=5/3.5
Vậy x=2.8
b) Ta có PQ // EF
Áp dụng định lý Talet trong tam giác DEF ta có: DP/PE= DQ/QF
Mà DP = x, PE = 10,5 ; DQ = 9 ; QF = DF – DQ = 24 – 9 = 15
Do đó ta có :
⇒ 15x = 9.10,5
⇔ 15x = 94,5
⇔ x = 94,5:15 = 6,3
Vậy x = 6,3.
Vừa rồi Chúng Tôi đã chia sẻ cho bạn định lý Talet trong tam giác và những hệ quả của nó. Đừng quên cập nhật những kiến thức mới qua bài viết sau của Chúng Tôi nhé!
Trên đây, chúng ta đã tìm hiểu về định lý Talet trong tam giác và những hệ quả quan trọng của định lý này. Định lý Talet đã chứng minh một mối liên hệ quan trọng giữa các đoạn thẳng trong tam giác, đó là:
1. Định lý Talet: “Trong tam giác ABC, độ dài của một đoạn thẳng bất kỳ nằm giữa hai đỉnh của tam giác là ngắn nhất khi nằm giữa hai đỉnh này trên đường thẳng đi qua đỉnh thứ ba, và dài nhất khi nằm trên đường thẳng đi qua đỉnh thứ ba và song song với đỉnh thứ ba.”
Định lý Talet đã giúp chúng ta hiểu rõ hơn về phương trình và tính chất của các đoạn thẳng trong tam giác. Nó cung cấp cho chúng ta một hướng dẫn cơ bản về cách tính toán và so sánh các độ dài trong tam giác, đồng thời mở ra nhiều hệ quả quan trọng. Hãy cùng điểm qua một số hệ quả quan trọng của định lý Talet:
2. Định lý cạnh bên: “Trong tam giác ABC, một cạnh nằm giữa hai góc bằng nhau là bằng nhau.”
Định lý cạnh bên là một hệ quả trực tiếp từ định lý Talet. Nếu ta có hai góc bằng nhau trong tam giác ABC, thì độ dài hai cạnh nằm giữa hai góc đó sẽ bằng nhau. Điều này cho phép chúng ta suy ra nhanh chóng độ dài của các cạnh trong tam giác chỉ dựa trên độ dài cạnh khác và góc tương ứng.
3. Định lý tam giác đều: “Trong tam giác ABC, nếu có hai cạnh bằng nhau thì các góc tương ứng với hai cạnh đó cũng bằng nhau.”
Định lý tam giác đều cũng là một hệ quả trực tiếp từ định lý Talet. Nếu ta có hai cạnh bằng nhau trong tam giác ABC, thì các góc tương ứng với hai cạnh đó cũng sẽ bằng nhau. Điều này cho phép chúng ta suy ra tam giác có các góc bằng nhau và từ đó có thể xác định dễ dàng hình dạng và tính chất của tam giác.
Tổng kết lại, định lý Talet là một trong những định lý quan trọng trong hình học tam giác, nó đã giúp chúng ta hiểu rõ hơn về mối quan hệ giữa các đoạn thẳng trong tam giác và từ đó suy ra được nhiều hệ quả quan trọng khác. Việc nắm vững định lý Talet và những hệ quả của nó sẽ giúp chúng ta giải quyết các bài toán liên quan đến tính chất và phương trình trong tam giác một cách hiệu quả.
Cảm ơn bạn đã xem bài viết Định lý Talet trong tam giác và những hệ quả của định lý tại thcshuynhphuoc-np.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Định lý Talet trong tam giác
2. Tam giác vuông và định lý Talet
3. Tính chất của tổng bình phương đường cao trong tam giác
4. Chứng minh của định lý Talet
5. Định lý Pitago và định lý Talet
6. Định lý Talet và tính chất của tam giác cân
7. Tam giác đều và định lý Talet
8. Tam giác tù và định lý Talet
9. Hệ quả của định lý Talet với đường cao
10. Ứng dụng của định lý Talet trong giải các bài toán tam giác
11. Hệ quả của định lý Talet với cạnh và góc trong tam giác
12. Định lý Talet và tính chất của tam giác vuông cân
13. Định lý Talet và tính chất của tam giác vuông nhọn
14. Hệ quả của định lý Talet với độ dài các cạnh trong tam giác
15. Định lý Talet và tính chất của tam giác vuông tù


