Bạn đang xem bài viết Dấu hiệu nhận biết hình thoi? Tính chất, các cách chứng minh tại thcshuynhphuoc-np.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Hình thoi là một trong những hình học cơ bản mà chúng ta thường gặp trong cuộc sống hàng ngày. Tuy nhiên, để nhận biết một hình thoi và hiểu rõ về các tính chất của nó không phải là điều dễ dàng đối với mọi người. Vì vậy, trong bài viết này, chúng ta sẽ cùng tìm hiểu về các dấu hiệu nhận biết hình thoi cũng như những tính chất độc đáo của nó và cách chứng minh chúng.
Đầu tiên, để nhận biết một hình thoi, chúng ta phải tìm hiểu về các đặc điểm đặc trưng của nó. Hình thoi có bốn cạnh có độ dài bằng nhau, cặp đường chéo chính bằng nhau và cắt nhau vuông góc tại trung điểm của mỗi đoạn. Điều này làm cho hình thoi trở nên dễ dàng phân biệt với các hình khác như hình chữ nhật hay hình vuông.
Tuy nhiên, chỉ riêng dựa vào các dấu hiệu đó không đủ để chứng minh một hình là hình thoi. Chúng ta cần có những bằng chứng cụ thể để khẳng định tính chất này. Một trong những cách chứng minh phổ biến nhất là sử dụng học hình học. Chúng ta có thể dùng định nghĩa của hình thoi kết hợp với các định lý và quy tắc trong học hình học để chứng minh tính chất của hình thoi, chẳng hạn như định lý Pitago, định lý tam giác bằng nhau hay định lý đối xứng.
Ngoài ra, chúng ta cũng có thể sử dụng phương pháp phân tích hình học để chứng minh tính chất của hình thoi. Ví dụ, chúng ta có thể sử dụng các công thức tính diện tích, chu vi hoặc đường chéo của hình thoi để kiểm tra tính chính xác của nó.
Một điểm đặc biệt quan trọng cần lưu ý là tính chất đối xứng của hình thoi. Điều này có nghĩa rằng nếu chúng ta biết một đường chéo của hình thoi, thì ta có thể dễ dàng xác định các đường chéo còn lại và các cạnh của nó.
Tóm lại, việc nhận biết và chứng minh tính chất của hình thoi là một nhiệm vụ quan trọng trong học hình học. Với những dấu hiệu nhận biết và phương pháp chứng minh đã được đề cập, chúng ta hy vọng sẽ có cái nhìn rõ ràng và chi tiết hơn về hình thoi và tính chất đặc biệt của nó.
Dấu hiệu nhận biết các hình là một trong những kiến thức quan trọng trong Toán học. Nó giúp cho bạn giải quyết những bài Toán chứng minh một cách dễ dàng. Vậy dấu hiệu nhận biết hình thoi là gì? Cùng Chúng Tôi tìm hiểu ngay nhé!
Dấu hiệu nhận biết hình thoi
Trước khi tìm hiểu về các dấu hiệu nhận biết hình thoi, bạn đọc của Chúng Tôi cần nắm rõ khái niệm về hình thoi ngay sau đây nhé!
Định nghĩa hình thoi
Hình thoi trong hình học Euclide là một tứ giác có 4 cạnh bằng nhau. Hình thoi cũng là một hình bình hành đặc biệt và có đầy đủ tính chất của hình bình hành.
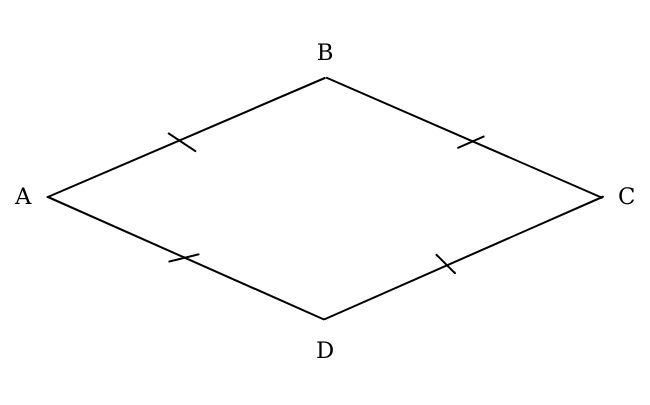
Hình thoi và các tính chất của hình thoi là một trong những kiến thức nền tảng về hình học trong Toán học. Vậy dấu hiệu nhận biết hình thoi là gì, mời bạn đọc theo dõi phần tiếp theo của bài viết nhé!
Dấu hiệu nhận biết hình thoi
Dưới đây là một số dấu hiệu nhận biết hình thoi mà Chúng Tôi đã tổng hợp, các bạn có thể tham khảo:
- Hình tứ giác đặc biệt là hình thoi nếu có các dấu hiệu nhận biết như sau:
- Tứ giác có 4 cạnh bằng nhau.
- Tứ giác có 2 đường chéo là đường trung trực của nhau.
- Tứ giác có 2 đường chéo là đường phân giác của cả 4 góc.
- Hình bình hành đặc biệt là hình thoi nếu có những đặc điểm dưới đây:
- Hình bình hành có 2 cạnh kề bằng nhau là hình thoi.
- Hình bình hành có 2 đường chéo vuông góc với nhau.
- Hình bình hành có 1 đường chéo là đường phân giác của một góc.
Trong Toán học, có rất nhiều dạng bài tập đòi hỏi bạn phải có sự suy luận. Chính vì thế, các dấu hiệu nhận biết hình thoi sẽ là kiến thức giúp ích cho bạn rất nhiều đấy!
Tính chất hình thoi
Tính chất hình thoi gồm 4 điều cơ bản sau:
- Hình thoi có các góc đối nhau bằng nhau.
- Hình thoi có hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
- Hình thoi có tất cả tính chất của hình bình hành.
- Trong hình thoi, hai đường chéo là các đường phân giác của các góc của hình thoi.
Những tính chất này góp phần quan trọng trong các bài Toán hình học. Chính vì thế, việc nắm rõ các tính chất cũng như dấu hiệu nhận biết hình thoi thì những bài Toán hình sẽ không thành vấn đề với bạn.
Xem thêm:
- Tính chất hình chữ nhật? 4 dấu hiệu nhận biết HCN
- Tính chất hình thang là gì? Tìm hiểu kiến thức hình thang
- Tính chất hình bình hành là gì? 7 bài tập liên quan
Các cách chứng minh hình thoi
Nếu bạn đã có đầy đủ kiến thức về dấu hiệu nhận biết hình thoi thì việc chứng minh một tứ giác hoặc một hình bình hành là hình thoi quả thật đơn giản với bạn phải không nào?
Dưới đây là một số cách chứng minh hình thoi mà Chúng Tôi tổng hợp, bạn có thể tham khảo:
Cách 1: Tứ giác có bốn cạnh bằng nhau
Ví dụ: Chứng minh rằng các trung điểm của bốn cạnh của một hình chữ nhật là các đỉnh của hình thoi.
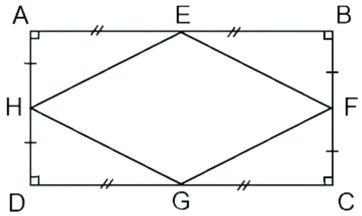
Ta có:
- AE = EB = ½ AB
- CG = GD = ½ CD
Mà AB = CD (ABCD là hình chữ nhật) (1)
⇒ EA = EB = GC = GD
Chứng minh tương tự, ta có: AH = BF = CF = DH
Xét Δ ABD có E và H lần lượt là trung điểm của AB và AD
⇒ EH là đường trung bình của ΔABD
⇒ EH = ½ BD (2)
Chứng minh tương tự, ta có EF = ½ AC; FG = ½ BD; HG = ½ AC (3)
Từ (1), (2), (3) ⇒ EF = FG = GH = HE
⇒ Tứ giác EFGH có 4 cạnh bằng nhau nên là hình thoi (đpcm).
Cách 2: Hình bình hành có hai đường chéo vuông góc
Ví dụ: Gọi O là giao điểm hai đường chéo của hình bình hành ABCD. Chứng minh rằng giao điểm các đường phân giác trong của các tam giác ΔAOB; ΔBOC; ΔCOD và ΔDOA là đỉnh của một hình thoi.
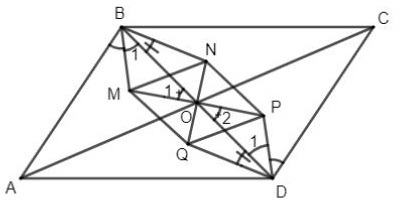
Gọi M, N, P, Q lần lượt là giao điểm các phân giác trong của các tam giác AOB, BOC, COD và DOA.
Vì O là giao điểm hai đường chéo AC và BD của hình bình hành ABCD nên OA = OC và OB = OD.
Xét Δ BMO và Δ DPO có:
Góc B1 = D1 và Góc O1 = O2 ( đối đỉnh ) và OB = OD (gt)
⇒ Δ BMO = ΔDPO (g – c – g)
⇒ OM = OP và các điểm M, O, P thẳng hàng (1)
Chứng minh tương tự: ON = OQ và N, O, P thẳng hàng (2)
Từ (1) và (2) ⇒ Tứ giác MNPQ là hình bình hành do các đường chéo cắt nhau tại trung điểm mỗi đường (3)
Mặt khác OM, ON là hai đường phân giác của hai góc kề bù nên OM ⊥ ON (4)
Từ (3) và (4) ⇒ MNPQ là hình thoi do là hình bình hành có hai đường chéo vuông góc (đpcm).
Cách 3: Tứ giác có 2 đường chéo là đường trung trực của nhau
Ví dụ: Cho hình bình hành ABCD có AB = AC. Kéo dài trung tuyến AM của ΔABC và lấy ME = MA. Chứng minh tứ giác ABEC là hình thoi.
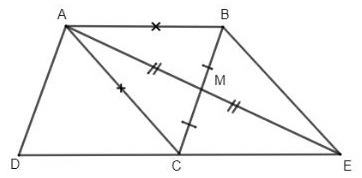
Ta có:
Δ ABC cân tại A có trung tuyến AM.
⇒ AM đồng thời là đường trung trực của BC.
⇒ Tứ giác ABEC là hình thoi do có 2 đường chéo là đường trung trực của nhau (đpcm).
Cách 4: Tứ giác là hình bình hành có hai cạnh kề bằng nhau
Ví dụ: Cho hình bình hành ABCD, có AD = DC. Chứng minh hình bình hành ABCD có 2 cạnh kề bằng nhau là hình thoi.
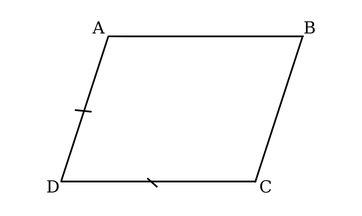
Ta có:
AB = CD (Tính chất hình bình hành)
AD = BC (Tính chất hình bình hành)
Mà AD = DC = AB = BC
⇒ ABCD là hình thoi vì có hai cạnh kề bằng nhau (đpcm).
Một số lưu ý khi làm bài tập về hình thoi
Bài tập về hình thoi gồm những dạng bài tập như sau:
- Chứng minh một hình là hình thoi.
- Tính chu vi hình thoi.
- Tính diện tích hình thoi.
Vì vậy những lưu ý khi làm bài tập về hình thoi bạn cần biết đó là nắm vững các kiến thức về dấu hiệu, tính chất cũng như công thức tính chu vi và diện tích hình thoi. Từ đó, các bạn áp dụng vào làm bài tập từ cơ bản đến nâng cao.
Khi bạn nhận biết những dấu hiệu như thế nào là hình thoi thì việc chứng minh trong Toán hình sẽ trở nên rất đơn giản.
Bài tập tham khảo về hình thoi
Bài 1: Chứng minh rằng giao điểm hai đường chéo của hình thoi là tâm đối xứng của hình thoi.
Hướng dẫn giải:
Hình bình hành nhận giao điểm hai đường chéo là tâm đối xứng.
Hình thoi cũng là một hình bình hành nên giao điểm hai đường chéo của hình thoi là tâm đối xứng của hình.
Bài 2: Cho hình thang cân ABCD . Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh rằng tứ giác MNPQ là hình thoi.
Hướng dẫn giải:
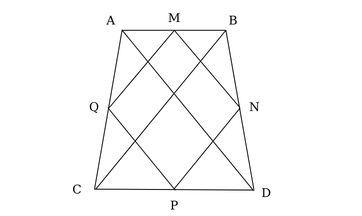
Trong Δ ABC, MN là đường trung bình nên ta có MN = ½ AC và MN // AC (1).
Tương tự trong tam giác ACD có: PQ = ½ AC và PQ // AC (2)
Từ (1) và (2) ⇒ MN = PQ và MN // PQ
Do vậy MNPQ là hình bình hành (3)
Xét Δ ABD ta có: MQ là đường trung bình ⇒ MQ = ½ BD
Vì ABCD là hình thang cân nên AC = BD
Từ đó suy ra MN = MQ (4)
Từ (1), (2), (3), (4) ⇒ MNPQ là hình thoi.
Bài 3: Cho tam giác ABC cân tại A, trung tuyến AM. Qua M kẻ đường thẳng song song với AC và cắt AB tại P và đường thẳng song song với AB cắt AC tại Q.
a. Tứ giác APMQ là hình gì? Vì sao?
b. Chứng minh PQ // BC
Hướng dẫn giải:
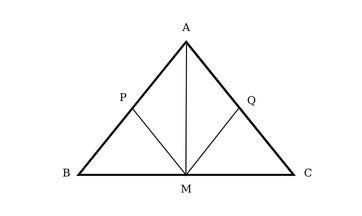
a. Xét Δ ABC có
M là trung điểm của BC (AM là đường trung tuyến ứng với cạnh đáy BC trong ΔABC).
⇒ MP//AC (1)
Do đó: P là trung điểm của AB (Định lí 1 về đường trung bình của tam giác).
⇒ AP = ½ AB (2)
Ta có: Δ ABC cân tại A (gt)
⇒ AB = AC (3)
Từ (1), (2) và (3) ⇒ AP = AQ
Xét tứ giác APMQ có:
MP // AQ (MP // AC, Q ∈ AC)
MQ // AP (MQ // AB, P ∈ AB)
Do đó: APMQ là hình bình hành (Dấu hiệu nhận biết hình bình hành)
Hình bình hành APMQ có AP = AQ (cmt)
⇒ APMQ là hình thoi (hình bình hành có 2 cạnh kề bằng nhau)
b. Ta có;
PQ ⊥ AM
AM ⊥ BC (tính chất tam giác cân)
⇒ PQ // BC
Trên đây là tất cả những thông tin kiến thức liên quan đến dấu hiệu nhận biết hình thoi. Hy vọng bài viết của Chúng Tôi có thể giúp bạn nắm rõ hơn về hình thoi. Chúc các bạn học tốt! Hãy truy cập Chúng Tôi mỗi ngày để thu nhận nhiều điều bổ ích nhé!
Trong bài viết này, chúng ta đã nghiên cứu về dấu hiệu nhận biết hình thoi, tính chất và các cách chứng minh của nó. từ đó, chúng ta có thể kết luận như sau:
Đầu tiên, dấu hiệu nhận biết chính để xác định một hình là hình thoi là có cạnh và góc. Hình thoi có cả bốn cạnh bằng nhau và cả bốn góc đều là góc vuông, điều này là dấu hiệu quan trọng để xác định hình thoi so với các hình khác.
Thứ hai, tính chất đặc trưng của hình thoi là sự đối xứng và sự cân đối. Đặc điểm đối xứng của hình thoi được thể hiện qua trục đối xứng đi qua hai đường chéo của nó, trong khi tính chất cân đối được thể hiện qua việc căn giữa các đường chéo của nó.
Cuối cùng, có nhiều cách chứng minh để xác định một hình là hình thoi. Một số phương pháp thông dụng bao gồm: sử dụng tính chất cân đối để xác định các góc và cạnh bằng nhau, sử dụng định nghĩa hình thoi đối với các điểm, sử dụng công thức diện tích và chu vi của hình thoi để kiểm tra sự tương quan giữa các giá trị, và sử dụng công cụ hình học để vẽ và kiểm tra tính chất của hình thoi.
Tổng kết lại, dấu hiệu nhận biết hình thoi, tính chất và các cách chứng minh của nó là những kiến thức cơ bản trong hình học. Việc hiểu và áp dụng chúng giúp chúng ta nhận biết và xác định chính xác các hình thoi trong thực tế và giải quyết các vấn đề liên quan đến hình học một cách chính xác.
Cảm ơn bạn đã xem bài viết Dấu hiệu nhận biết hình thoi? Tính chất, các cách chứng minh tại thcshuynhphuoc-np.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Hình thoi
2. Đường chéo
3. Đối xứng
4. Cặp đường chéo bằng nhau
5. Cặp đường chéo cắt nhau vuông góc
6. Cặp cạnh bằng nhau
7. Bậc hai
8. Góc
9. Đường kính
10. Điểm nằm trên đường kính cắt nhau vuông góc
11. Điểm nằm trên đường kính cắt nhau ở trung điểm
12. Bình phương
13. Tâm
14. Bán kính
15. Dạng chuyển đổi đồng biến và nghịch biến


