Bạn đang xem bài viết Cách tính chu vi hình tam giác – Giải bài tập SGK Toán 3 tại thcshuynhphuoc-np.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Chu vi là một thuộc tính quan trọng trong hình học và việc tính chu vi của các hình học đặc biệt như tam giác luôn là một bài toán thú vị cho các em học sinh. Trong chương trình giáo dục Toán lớp 3, việc tính chu vi của tam giác là một trong những kiến thức cơ bản mà các em phải nắm vững.
Cách tính chu vi hình tam giác có thể được giải bài tập trong sách giáo trình Toán 3 là một khía cạnh quan trọng trong việc xây dựng kiến thức toán học của các em. Trong bài viết này, chúng ta sẽ cùng nhau tìm hiểu về cách tính chu vi của tam giác và giải một số bài tập trong sách giáo kèm theo.
Để tính chu vi của tam giác, chúng ta cần biết các đặc điểm cơ bản của tam giác. Tam giác là một hình học có ba cạnh và ba đỉnh. Để tính chu vi của tam giác, ta cộng độ dài của ba cạnh lại với nhau.
Với mỗi bài tập trong sách giáo trình Toán 3, chúng ta sẽ nhìn vào hình vẽ tam giác đã cho, và dựa vào độ dài của các cạnh được cho (hoặc các đối tượng được định nghĩa trong các bài tập), chúng ta có thể tính được chu vi của tam giác.
Các dạng bài toán tính chu vi, diện tích hình tam giác, hình chữ nhật, hình vuông xuất hiện rất nhiều trong bài thi Toán cấp 1. Vậy để làm tốt bài tập, các bạn học sinh cần nắm rõ công thức tính chu vi, diện tích các hình.
Bài viết hôm nay của Chúng Tôi sẽ hướng dẫn bạn cách tính chu vi hình tam giác và các dạng bài tập có liên quan. Cùng theo dõi bạn nhé!
Cách tính chu vi hình tam giác
Có 4 loại tam giác cơ bản là tam giác thường, tam giác cân, tam giác vuông và tam giác đều. Mỗi dạng tam giác đều có cách tính chu vi khác nhau. Cùng tìm hiểu nhé!
Cách tính chu vi hình tam giác thường
Tam giác thường là loại tam giác cơ bản nhất, có độ dài các cạnh khác nhau, số đo góc trong cũng khác nhau.
Công thức tính chu vi hình tam giác thường: P = a + b + c
Trong đó:
- P là chu vi tam giác
- a, b, c lần lượt là độ dài 3 cạnh của tam giác
Diễn đạt bằng lời: Chu vi tam giác bằng độ dài tổng ba cạnh của tam giác đó.
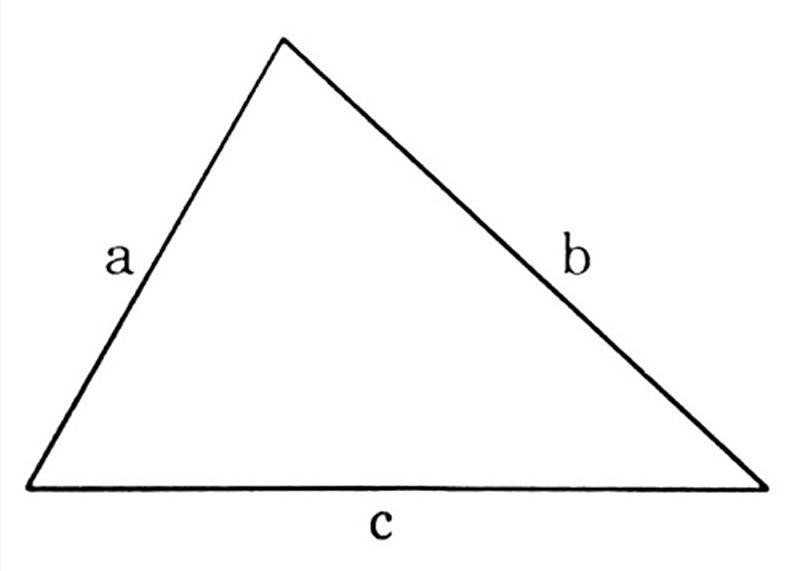
Ví dụ: Cho tam giác có độ dài 3 cạnh lần lượt là 4cm, 8cm và 9cm. Tính chu vi hình tam giác đó.
Giải: Dựa vào công thức ta có chu vi hình tam giác đó là:
P = 4 + 8 + 9 = 21 cm.
Cách tính chu vi hình tam giác cân
Tam giác cân là tam giác có 2 cạnh, 2 góc bằng nhau. Đỉnh của tam giác cân là giao điểm của 2 cạnh bên.
Công thức tính chu vi hình tam giác cân: P = 2.a + c
Trong đó:
- a là độ dài hai cạnh bên của tam giác cân
- c là độ dài cạnh đáy của tam giác
Diễn đạt bằng lời: Chu vi tam giác cân bằng 2 lần cạnh bên cộng với cạnh đáy.
Lưu ý: Công thức tính chu vi hình tam giác này cũng được áp dụng để tính chu vi của tam giác vuông cân (tam giác có 1 góc vuông và 2 cạnh bên bằng nhau).
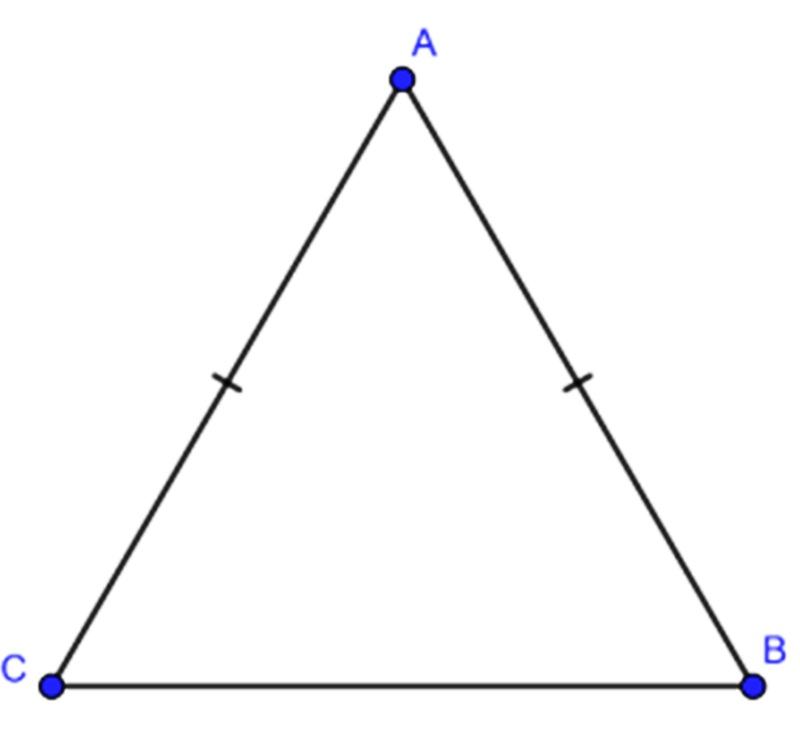
Ví dụ: Tính chu vi tam giác cân ABC khi biết chiều dài cạnh bên là 5 cm, chiều dài cạnh đáy là 8cm.
Giải:
Áp dụng công thức tính chu vi hình tam giác, ta có:
Chu vi tam giác ABC là:
P (ABC) = 2.a + c = (2 x 5) + 8 = 18 (cm).
Cách tính chu vi hình tam giác đều
Tam giác đều là tam giác có 3 cạnh bằng nhau, là trường hợp đặc biệt của tam giác cân.
Công thức tính chu vi hình tam giác đều: P = a + a + a = 3 x a
Trong đó:
- P là chu vi tam giác đều
- a là độ dài cạnh của tam giác
Diễn đạt bằng lời: Chu vi tam giác đều bằng tổng độ dài ba cạnh, mà ba cạnh của tam giác bằng nhau nên tức là bằng độ dài một cạnh nhân ba.
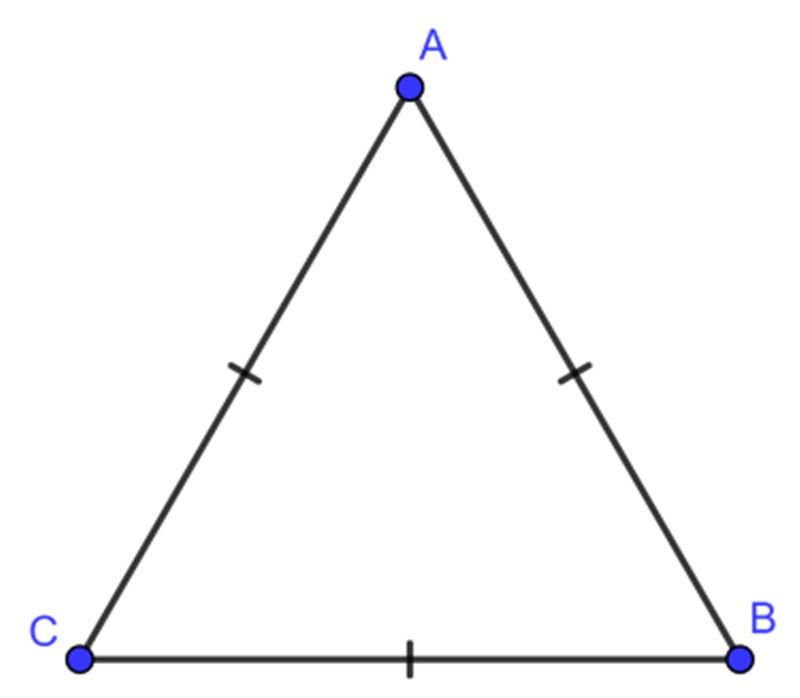
Ví dụ: Tính chu vi tam giác đều ABC với chiều dài cạnh AB = 5 cm.
Vì tam giác ABC là tam giác đều nên ta có, độ dài các cạnh là: AB = AC = BC = 5cm
Dựa vào công thức tính chu vi tam giác đều, ta có:
P (ABC) = 5 x 3 = 15 cm
Cách tính chu vi hình tam giác vuông
Tam giác vuông là tam giác có 1 góc bằng 90°.
Công thức tính chu vi hình tam giác vuông:
P = a + b + c
Trong đó:
- a và b là độ dài hai cạnh của tam giác vuông.
- c là độ dài cạnh huyền của tam giác vuông.
Diễn đạt bằng lời: Chu vi hình tam giác vuông bằng tổng chiều dài 3 cạnh của tam giác.
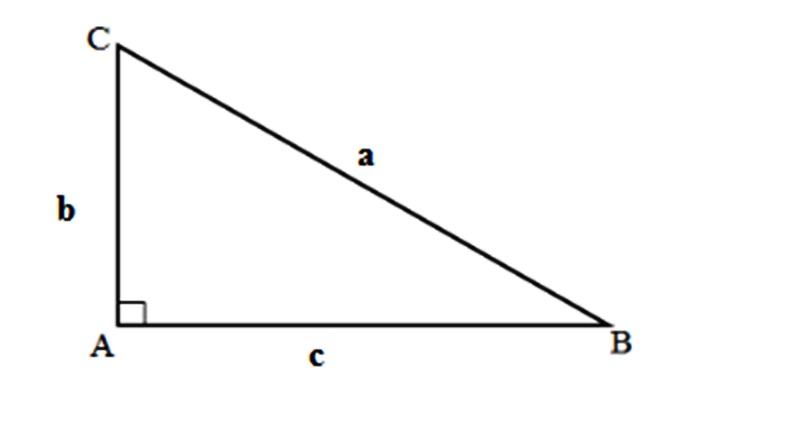
Ví dụ: Cho tam giác vuông ABC với độ dài 3 cạnh lần lượt là 3 cm, 4 cm và 5 cm. Hãy tính chu vi của tam giác vuông.
Giải:
Dựa theo công thức, ta có chu vi tam giác vuông ABC là:
P (ABC) = 3 + 4 + 5 = 12 (cm)
Giải bài tập cách tính chu vi hình tam giác
Sau khi đã tìm hiểu cách tính chu vi hình tam giác, bạn hãy cùng Chúng Tôi giải các bài tập liên quan để nắm vững kiến thức nhé!
Bài tập cách tính chu vi hình tam giác lớp 3
Giải bài 2 trang 174 – SGK Toán lớp 3 tập 1
Tính chu vi hình tam giác có độ dài các cạnh là 35 cm, 26 cm, 40 cm.
Giải:
Chu vi tam giác là:
35 + 26 + 40 = 101(cm)
Đáp số: 101 cm
Giải bài 4 trang 9 – SGK Toán lớp 3 tập 1
Tính chu vi tam giác ABC có kích thước ghi trên hình vẽ:
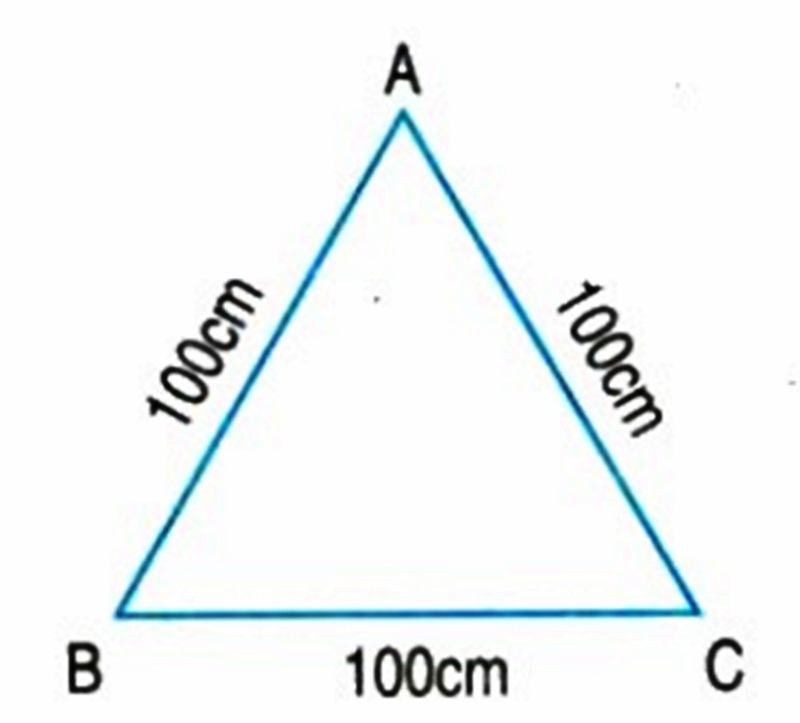
Giải:
Chu vi hình tam giác ABC là:
100 + 100 + 100 = 300 (cm)
Đáp số: 300 cm
Bài tập cách tính chu vi hình tam giác lớp 4
Giải bài 4 trang 44 – SGK Toán lớp 4 tập 1
Độ dài các cạnh của hình tam giác là a, b, c.
a) Gọi P là chu vi của hình tam giác.
Viết công thức tính chu vi P của hình tam giác đó.
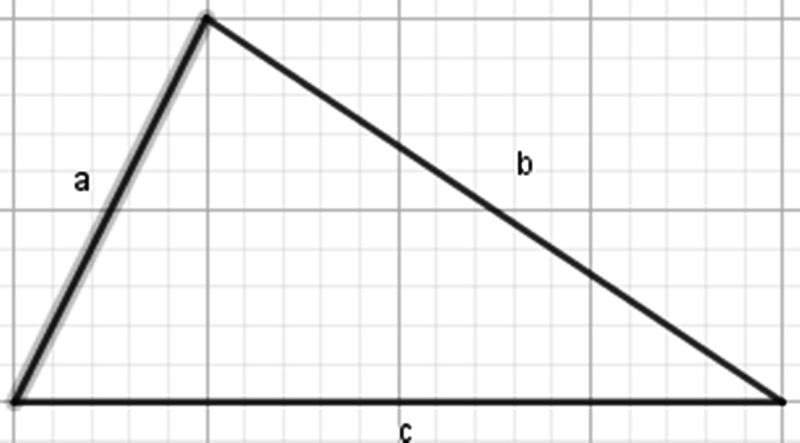
b) Tính chu vi của hình tam giác biết:
a = 5 cm, b = 4 cm và c = 3 cm;
a = 10 cm, b = 10 cm và c = 5 cm;
a = 6 dm, b = 6 dm và c = 6 dm.
Giải:
a) Công thức tính chu vi P của tam giác là :
P = a + b + c.
b) Nếu a = 5cm, b = 4cm và c = 3cm thì P = 5cm + 4cm + 3cm = 12cm.
Nếu a = 10cm, b = 10cm và c = 5cm thì P = 10cm + 10cm + 5cm = 25cm.
Nếu a = 6dm, b = 6dm và c = 6dm thì P = 6dm + 6dm + 6dm = 18dm.

Xem thêm: Tính chất trọng tâm tam giác và cách xác định trọng tâm
Hy vọng bài viết trên của Chúng Tôi đã giúp bạn nắm vững kiến thức về cách tính chu vi hình tam giác. Bạn hãy luyện tập nhiều hơn để làm bài thật tốt nhé. Hẹn gặp lại bạn ở bài viết sau!
Trên đây là những kiến thức cơ bản về cách tính chu vi hình tam giác và một số bài tập liên quan được giải trong sách giáo trình Toán 3. Chúng ta đã tìm hiểu về cách tính chu vi tam giác chỉ bằng độ dài các cạnh, cùng với một số cách tính chu vi khác khi biết thông tin khác về tam giác. Ngoài ra, chúng ta cũng đã làm quen với việc sử dụng công thức tính chu vi hình tam giác.
Việc tính chu vi hình tam giác không chỉ giúp chúng ta có cái nhìn tổng quan về kích thước của tam giác mà còn giúp phát triển kỹ năng tính toán và tư duy hình học của chúng ta. Bằng cách áp dụng những kiến thức đã học, chúng ta có thể giải quyết một số bài toán thực tế liên quan đến tam giác như tính số hàng rào cần xây dựng, tính chu vi đồng hồ cát, và nhiều bài toán khác.
Nhưng để trở thành một người giỏi trong việc tính toán chu vi tam giác, chúng ta cần nắm vững kiến thức và rèn luyện thực hành thường xuyên. Đây chỉ là những bước đầu tiên trong hành trình khám phá về tam giác và hình học nói chung. Việc tiếp tục tìm hiểu và rèn luyện kỹ năng sẽ giúp chúng ta vươn lên tầm cao mới và ứng dụng những kiến thức này vào thực tế một cách linh hoạt và sáng tạo hơn.
Tóm lại, việc tính chu vi hình tam giác là một kỹ năng cơ bản trong Toán 3. Nhờ kiến thức về công thức và quy tắc tính chu vi tam giác chúng ta có thể giải quyết được nhiều bài tập liên quan. Tuy nhiên, việc thành thạo và sáng tạo trong việc tính toán chu vi tam giác cần sự rèn luyện và khám phá tiếp cận.
Cảm ơn bạn đã xem bài viết Cách tính chu vi hình tam giác – Giải bài tập SGK Toán 3 tại thcshuynhphuoc-np.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Chu vi hình tam giác
2. Tính chu vi tam giác
3. Công thức tính chu vi tam giác
4. Cách tính chu vi tam giác vuông
5. Chu vi tam giác đều
6. Chu vi tam giác cân
7. Tính chu vi tam giác bằng độ dài ba cạnh
8. Công thức tính chu vi tam giác bằng độ dài cạnh và chiều cao
9. Công thức tính chu vi tam giác bằng các góc của tam giác
10. Giải bài tập tính chu vi tam giác
11. Chu vi tam giác vuông góc
12. Cách tính chu vi tam giác bằng độ dài cạnh và bán kính đường tròn ngoại tiếp
13. Tính chu vi tam giác bằng diện tích và bán kính đường tròn ngoại tiếp
14. Chu vi tam giác nhọn
15. Chu vi tam giác tù


