Bạn đang xem bài viết Bảng công thức đạo hàm nguyên hàm đầy đủ chi tiết tại thcshuynhphuoc-np.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
“Đạo hàm là một khái niệm quan trọng trong toán học và giải tích, đóng vai trò quan trọng trong việc tính toán và tìm hiểu các hàm số. Đạo hàm của một hàm số cho biết tốc độ thay đổi của hàm số đó tại mỗi điểm. Tuy nhiên, đôi khi chúng ta muốn tìm lại hàm ban đầu từ đạo hàm đã biết, và đó là lúc nguyên hàm xuất hiện.
Bảng công thức đạo hàm nguyên hàm đầy đủ chi tiết là một công cụ hữu ích giúp chúng ta tính toán nguyên hàm của nhiều hàm số phổ biến. Bảng này bao gồm các công thức đạo hàm của các hàm số cơ bản như hằng số, hàm mũ, hàm lượng giác, hàm logarit, và nhiều hàm số phức tạp hơn nữa. Điều này giúp chúng ta tiết kiệm thời gian và công sức trong việc tính toán, đồng thời cung cấp một cách tiếp cận dễ hiểu và rõ ràng để giải quyết các bài toán liên quan đến nguyên hàm.
Sự hiểu biết về bảng công thức đạo hàm nguyên hàm đầy đủ chi tiết cũng giúp chúng ta phát triển khả năng tư duy và logic trong việc xác định nguyên hàm của một hàm số nào đó. Nó cũng mang lại sự hiểu biết sâu hơn về các quy tắc và thuật toán trong giải tích.
Trong bài viết này, chúng ta sẽ tìm hiểu và khám phá bảng công thức đạo hàm nguyên hàm đầy đủ chi tiết. Chúng ta sẽ đi qua từng công thức một, đánh giá sự áp dụng của chúng và cách áp dụng chúng vào việc tính toán các nguyên hàm. Đồng thời, chúng ta cũng sẽ thấy được sự tương quan và tác động của các công thức này trên các hàm số cụ thể.
Bằng việc nắm vững các công thức đạo hàm nguyên hàm đầy đủ chi tiết, chúng ta có thể nâng cao khả năng giải quyết bài toán và hiểu sâu về tính chất của các hàm số. Đây là một công cụ hữu ích không chỉ trong lĩnh vực toán học mà còn trong các lĩnh vực ứng dụng khác như vật lý, kinh tế, và xã hội học.”
Đạo hàm nguyên hàm là kiến thức toán học quan trọng xuất hiện trong chương trình trung học phổ thông. Đây là các kiến thức quan trọng mà học sinh phải nắm vững nhằm giải toán chính xác, hiệu quả. Cùng ôn tập kiến thức qua bảng công thức đạo hàm nguyên hàm đầy đủ chi tiết mà chúng tôi đề cập bên dưới. Chắc chắn sẽ hữu ích và cần thiết cho các bạn học sinh.


Đạo hàm là gì?
Trong toán học, đạo hàm của hàm số là mô tả sự biến thiên của hàm số tại một điểm cụ thể nào đó. Đạo hàm là một khái niệm cơ bản trong chương trình toán học giải tích.
Nguyên hàm là gì?
Trong giải tích thì nguyên hàm hàm số thực cho trước f là một hàm F có đạo hàm bằng f, vậy F′ = f. Quá trình chúng ta đi tìm nguyên hàm gọi là tích phân bất định. Xác định biểu thức cho nguyên hàm khó hơn so với việc tìm đạo hàm.
Bảng công thức đạo hàm cơ bản
Học sinh cần ghi nhớ bảng công thức đạo hàm cơ bản áp dụng cho các bài toán cơ bản.


Hai hàm phân thức hữu tỉ có đạo hàm:

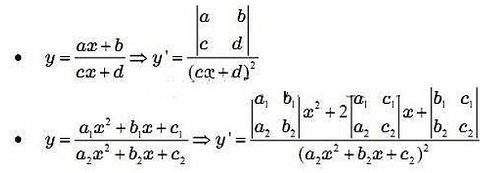


Quy tắc đạo hàm của hàm số hợp: Nếu y = y(u(x)) thì y'(x) = y'(u) . u'(x).
Đạo hàm của hàm số sơ cấp


Bảng đạo hàm cấp cao:

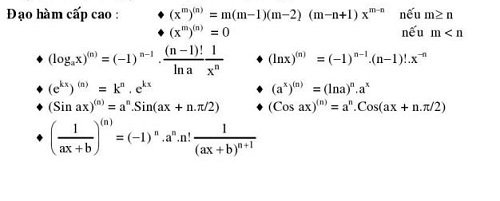
Bảng công thức nguyên hàm
Tính chất của nguyên hàm:

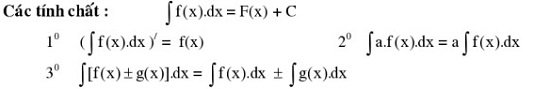
Bảng nguyên hàm cơ bản

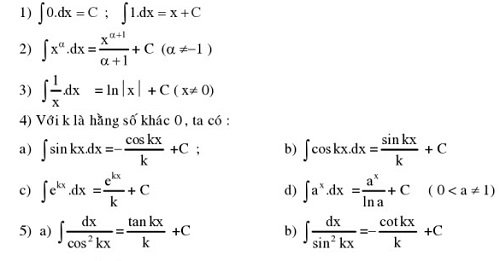
Bảng nguyên hàm mở rộng

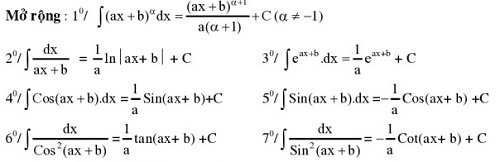
Phương pháp đổi biến số:

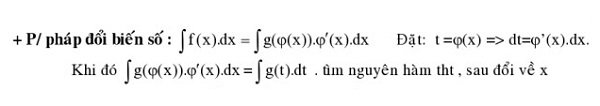
Phương pháp tích phân từng phần:

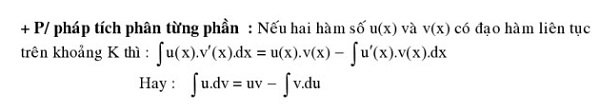
Mẹo ghi nhớ đạo hàm
Đạo hàm với các công thức thường gây khó khăn cho học sinh, vì vậy bài thơ bên dưới sẽ giúp các bạn ghi nhớ tốt hơn phần đạo hàm.










Bài thơ được sáng tạo nhằm giúp các em học sinh ghi nhớ tốt bảng đạo hàm, từ đó giải toán hiệu quả và chính xác.
Các dạng toán nguyên hàm
Bài toán 1: Phương pháp đổi biến số dạng 1 tìm nguyên hàm I = ∫f(x)dx
* Phương pháp:
– Bước 1: Chọn x = φ(t), φ(t) là hàm số chúng ta chọn.
– Bước 2: Lấy vi phân 2 vế, dx = φ'(t)dt.
– Bước 3: Biểu thị f(x)dx theo t và dt: f(x)dx = f[φ(t)].φ'(t)dt = g(t)dt.
– Bước 4: I = ∫g(t)dt = G(t) + C
Bài toán 2: Phương pháp đổi biến số dạng 2 tìm nguyên hàm I = ∫f(x)dx
* Phương pháp:
– Bước 1: Chọn t = ψ(x), với ψ(x) là hàm số phù hợp.
– Bước 2: Vi phân 2 vế: dt = ψ'(x)dx.
– Bước 3: Biểu thị f(x)dx theo t và dt: f(x)dx = f[φ(t)].φ'(t)dt = g(t)dt.
– Bước 4: I = ∫g(t)dt = G(t) + C
Các bạn vừa theo dõi bảng công thức đạo hàm nguyên hàm đầy đủ và phương pháp ghi nhớ đạo hàm qua bài thơ. Các dạng toán nguyên hàm và phương pháp giải hiệu quả. Các kiến thức này rất quan trọng với học sinh 12, hãy nắm vững kiến thức và ôn tập để giải các bài toán một cách hiệu quả và điểm số cao trong kiểm tra.
Xem thêm: Các công thức lượng giác
Chúc các bạn học tốt môn Toán!
Trên thực tế, bảng công thức đạo hàm nguyên hàm đầy đủ chi tiết là một công cụ hữu ích trong toán học và các lĩnh vực liên quan. Bảng công thức này cung cấp cho chúng ta một danh sách các công thức dựa trên quy tắc đạo hàm để tính toán nguyên hàm của một hàm.
Sử dụng bảng công thức đạo hàm nguyên hàm đầy đủ chi tiết, chúng ta có thể tìm ra một phương trình cho một hàm dựa trên công thức đạo hàm của nó. Điều này giúp chúng ta thực hiện tính toán một cách chính xác và nhanh chóng.
Bảng công thức đạo hàm nguyên hàm đầy đủ chi tiết bao gồm các công thức cơ bản nhất như đạo hàm của hàm số mũ, đạo hàm của hàm lũy thừa, đạo hàm của hàm hằng số, và còn nhiều công thức khác. Bảng này cũng có thể bao gồm những công thức phức tạp hơn như quy tắc chuỗi, quy tắc ứng dụng lần kéo dài và quy tắc tích phân.
Bảng công thức đạo hàm nguyên hàm đầy đủ chi tiết là một công cụ lý thuyết quan trọng cho việc nghiên cứu và áp dụng toán học. Nó được sử dụng trong nhiều lĩnh vực khác nhau như vật lý, kỹ thuật, kinh tế học và xác suất thống kê.
Tuy nhiên, mặc dù bảng công thức đạo hàm nguyên hàm đầy đủ chi tiết là một công cụ hữu ích, việc sử dụng nó đòi hỏi có kiến thức về toán cao cấp và kỹ năng chính xác trong việc áp dụng các công thức. Điều này đòi hỏi sự chú ý và cẩn thận để tránh mắc phải lỗi tính toán và kết quả sai sót trong quá trình tính toán.
Tổng kết lại, bảng công thức đạo hàm nguyên hàm đầy đủ chi tiết là một công cụ quan trọng trong việc tính toán và nghiên cứu các công thức đạo hàm. Nó giúp ta làm việc một cách chính xác và nhanh chóng, tuy nhiên, việc sử dụng nó đòi hỏi kiến thức và kỹ năng toán học cao cấp.
Cảm ơn bạn đã xem bài viết Bảng công thức đạo hàm nguyên hàm đầy đủ chi tiết tại thcshuynhphuoc-np.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Đạo hàm
2. Nguyên hàm
3. Bảng công thức
4. Chi tiết
5. Đầy đủ
6. Chủ đề
7. Từ khoá
8. Công thức
9. Toán học
10. Hàm số
11. Dạng tổng quát
12. Đối số
13. Hàm lượng giác
14. Hàm số đa thức
15. Bài tập

