Tính chất đường trung tuyến? 2 dạng bài tính chất đường trung tuyến cơ bản

Nhắc đến tính chất đường trung tuyến, ắt hẳn vẫn còn nhiều bạn học sinh chưa nắm vững được kiến thức quan trọng này. Đừng quá lo lắng, bài viết sau của Chúng Tôi chính là dành cho bạn. Cùng đi tìm hiểu tất cả thông tin, bài tập về tính chất đường trung tuyến nhé!

Đường trung tuyến là gì?

Đường trung tuyến của một đoạn thẳng là một đường thẳng đi qua trung điểm của đoạn thẳng đó. Trung điểm là điểm chia đoạn thẳng thành hai phần bằng nhau.

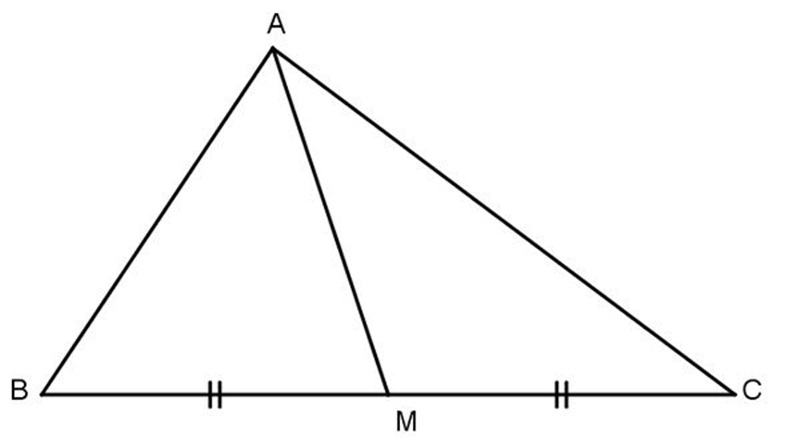
Đường trung tuyến trong tam giác là đoạn thẳng nối từ đỉnh của tam giác tới trung điểm của cạnh đối diện. Mỗi tam giác đều có ba đường trung tuyến.

Đối với tam giác cân và tam giác đều, mỗi trung tuyến của tam giác chia đôi các góc ở đỉnh với hai cạnh kề có chiều dài bằng nhau.

Tính chất đường trung tuyến của tam giác

Tính chất đường trung tuyến của tam giác là một phần kiến thức quan trọng để áp dụng trong nhiều bài tập hình học. Cùng ôn lại đường trung tuyến của tam giác có những tính chất cơ bản gì nhé!

Đồng quy tại 1 điểm

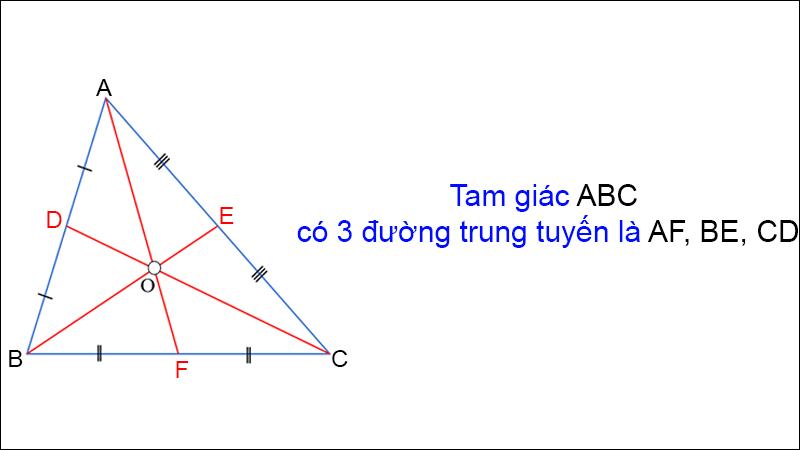
Ba đường trung tuyến của một tam giác cùng đi qua một điểm. Điểm đó cách đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy.

Giao điểm của ba đường trung tuyến gọi là trọng tâm

Ví dụ: Tam giác ABC có D, E, F lần lượt là trung điểm của ba cạnh BC, AC, AB và G là trọng tâm.

 

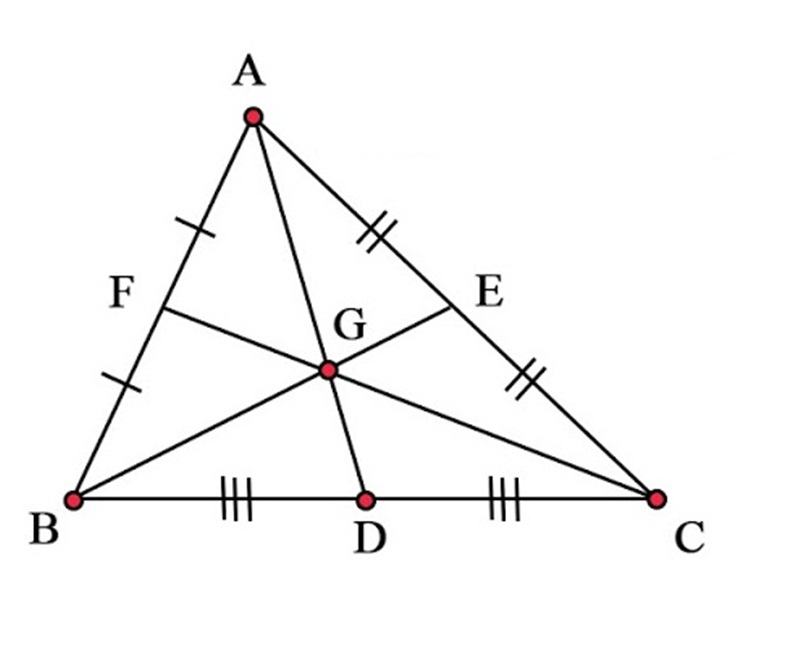
Vị trí trọng tâm của tam giác

Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy.

Chia thành các tam giác nhỏ có diện tích bằng nhau

Mỗi đường trung tuyến chia diện tích của tam giác thành hai phần bằng nhau. Ba trung tuyến chia tam giác thành sáu tam giác nhỏ với diện tích bằng nhau.

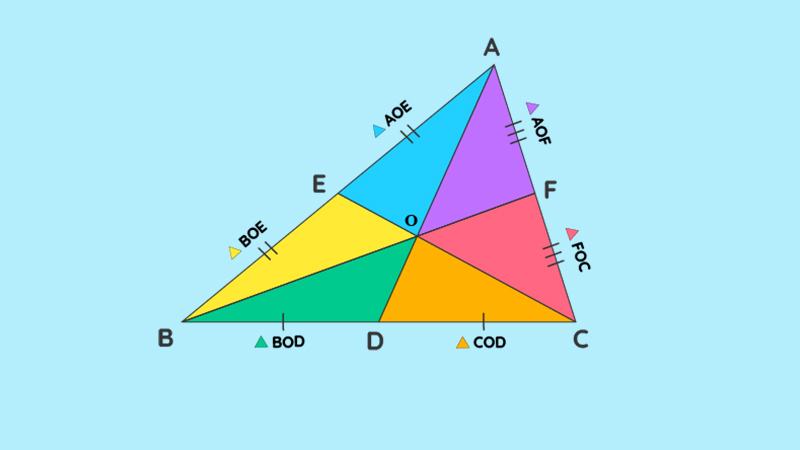
Định nghĩa đường trung tuyến trong tam giác đặc biệt

Không chỉ ở tam giác thường mà ở tam giác vuông, tam giác cân, tam giác đều cũng có tính chất của đường trung tuyến. Vậy tính chất đường trung tuyến trong tam giác đặc biệt là gì? Cùng Chúng Tôi ôn tập nhé!

Đường trung tuyến trong tam giác vuông

Trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền thì bằng nửa cạnh huyền.

Ngược lại, một tam giác có đường trung tuyến ứng với một cạnh mà bằng nửa cạnh đó thì tam giác ấy là tam giác vuông.

Ví dụ:

Tam giác ΔABC vuông ở A (như hình).

Độ dài đường trung tuyến AD sẽ bằng DB, DC và bằng 1/2. BC.

Ngược lại nếu AD = 1/2. BC thì tam giác ΔABC sẽ vuông ở A.

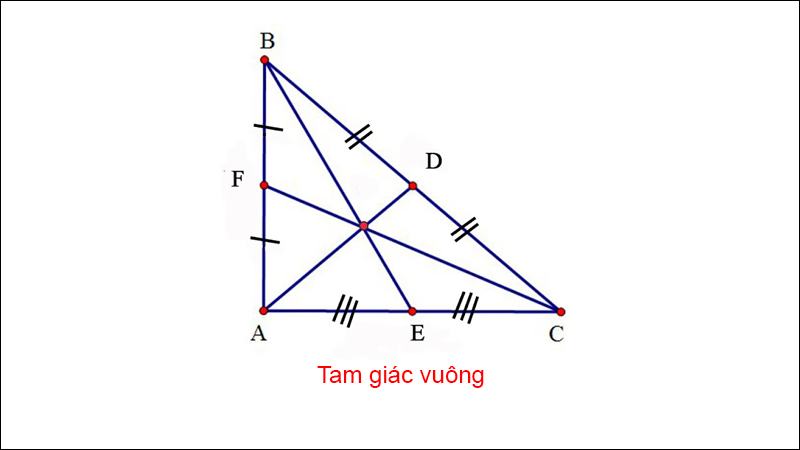
Đường trung tuyến trong tam giác cân, tam giác đều

Trong tam giác cân, tam giác đều, đường trung tuyến ứng với cạnh đáy thì vuông góc với cạnh đáy. Và nó chia tam giác lớn thành hai tam giác nhỏ bằng nhau.

Ví dụ:

Tam giác đều ΔABC có AD, BF, CE lần lượt là ba đường trung tuyến của tam giác (như hình).

Theo tính chất của đường trung tuyến trong tam giác đều ta có:

AD⊥BC; BF⊥AC; CE⊥AB

và ΔABD = ΔADC; ΔABF = ΔFBC; ΔAEC = ΔECB.

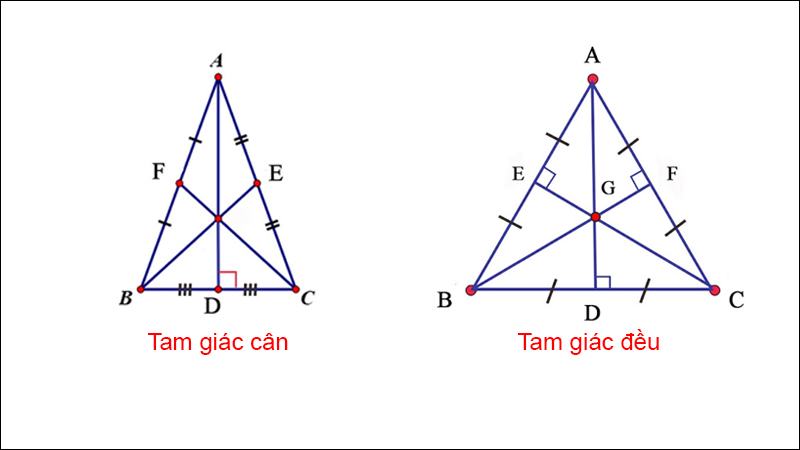
Một số công thức liên quan đến độ dài trung tuyến

Sau khi đã hiểu được định nghĩa về tính chất đường trung tuyến thì bạn cần nắm được công thức tính độ dài đường trung tuyến để làm tốt các bài tập nhé. Độ dài đường trung tuyến của một tam giác được tính thông qua độ dài các cạnh của tam giác.

Sử dụng định lý Apollonius để tính độ dài của trung tuyến như sau:

Trong đó:

• • a, b, c: là các cạnh của tam giác.

• • ma, mb, mc: là các đường trung tuyến của tam giác ứng với các cạnh a, b, c.

Một số dạng bài liên quan đến tính chất đường trung tuyến

Liên quan đến tính chất đường trung tuyến, Chúng Tôi sẽ tổng hợp một số dạng bài liên quan để giúp bạn luyện tập và hệ thống lại kiến thức nhé!

Dạng 1: Tìm tỉ lệ giữa các cạnh và tính độ dài của đoạn thẳng

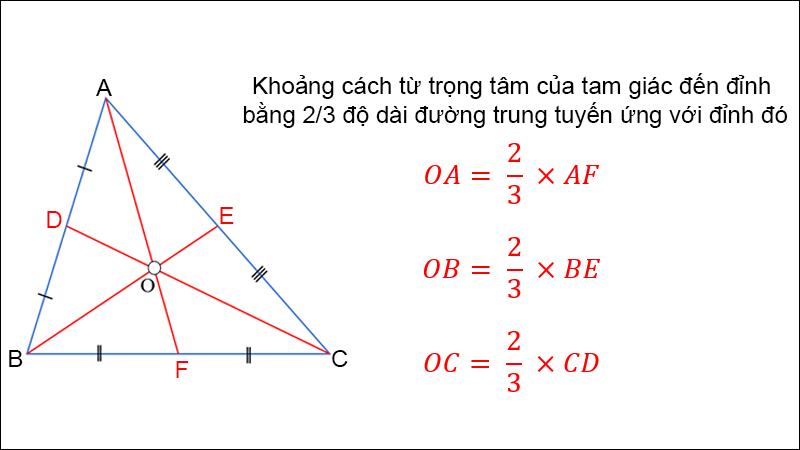
Với dạng toán này, bạn cần tập trung vào vị trí trọng tâm của tam giác và áp dụng định lý:

Khoảng cách từ trọng tâm của tam giác đến đỉnh bằng 2/3 độ dài đường trung tuyến ứng với đỉnh đó.

Với G là trọng tâm của tam giác ABC với AD, BE và CF lần lượt là 3 trung tuyến, lúc này ta có:

 

Bài tập ví dụ:

Bài 1:

Tam giác ABC có trung tuyến AM = 9cm và trọng tâm G. Tính độ dài đoạn thẳng AG?

Lời giải:

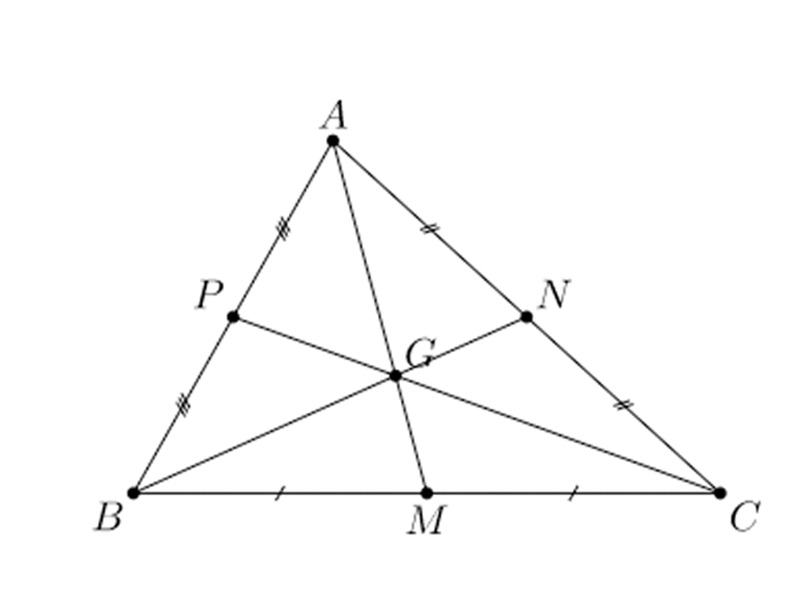
Vì G là trọng tâm tam giác ABC và AM là đường trung tuyến nên:

AG = 2/3 AM (tính chất ba đường trung tuyến của tam giác)

Do đó: AG = 2/3. 9 = 6cm

Vậy AG = 6cm.

Bài 2:

Cho tam giác ABC với G là trọng tâm. Trên cạnh AG lấy điểm G’ sao cho G là trung điểm của đoạn AG’. Yêu cầu so sánh:

a. Những cạnh của tam giác BGG’ với các đường trung tuyến của tam giác ABC.

b. Những đường trung tuyến của tam giác BGG’ với các cạnh của tam giác ABC.

Lời giải:

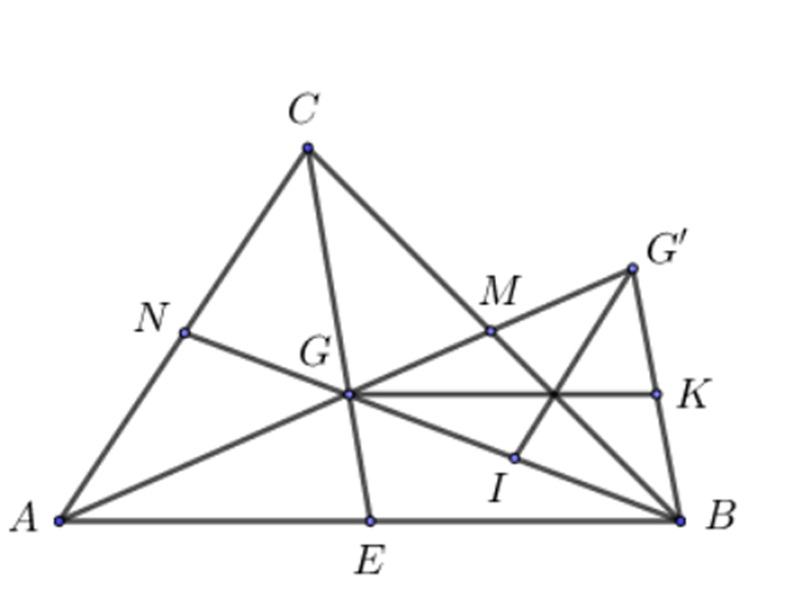
a. Ta có BG cắt AC tại điểm N, CG cắt AB tại điểm E và G là trọng tâm của tam giác ABC.

⇒ GA = 2/3 AM

Vì G là trung điểm của AG’ ⇒ GA =GG’

Suy ra: GG’ = 2/3 AM

Theo giả thuyết ta có G là trọng tâm của tam giác ABC

⇒ GB = 2/3 BN

Mặt khác: GM = 1/2 AG (vì G là trọng tâm)

AG = GG ‘ ⇒ GM = 1/2 GG’

M là trung điểm của đoạn GG’

Vì GM = MG’ và MB = MC ⇒ Tam giác GMC = tam giác G’MB

Suy ra: BG’ = CG

Mà CG = 2/3 CE (G là trọng tâm của tam giác ABC)

⇒ BG ‘= 2/3 CE

Vậy mỗi cạnh của tam giác BGG’ bằng 2/3 các đường trung tuyến của tam giác ABC.

b. Ta có BM là đường trung tuyến của tam giác BGG’

Mà điểm M lại là trung điểm của đoạn BC nên BM = 1/2 BC

I là trung điểm của BG ⇒ IG = 1/2 BG

G là trọng tâm tam giác ABC ⇒ GN = 1/2 BG

Suy ra: IG = GN

⇒ Tam giác IGG’ = tam giác NGA theo trường hợp cạnh – góc – cạnh

⇒ IG ‘= AN => IG’ = 1/2 AC

Gọi K là trung điểm của đoạn BG ⇒ GK là trung tuyến của tam giác BGG’

Mặt khác, vì G là trọng tâm của tam giác ABC ⇒ GE = 1/2 GC

Mà K là trung điểm của BG’ ⇒ KG” = EG

Vì tam giác GMC = tam giác G’BM (chứng minh trên)

⇒ Tam giác GCM = tam giác G’BM theo trường hợp góc so le trong

⇒ CE//BG ⇒ tam giác AGE = tam giác AG’B theo trường hợp đồng vị

Do đó tam giác AGE = tam giác GG’K (c.g.c) ⇒ AE = GK

Mà AE = 1/2 AB nên GK = 1/2 AB

Vậy mỗi đường trung tuyến của tam giác BGG’ bằng ½ các cạnh của tam giác ABC.

Bài 3:

Cho tam giác ABC có các đường trung tuyến BD và CE vuông góc với nhau. Tính độ dài cạnh BC biết BD = 9 cm và CE = 12 cm.

Lời giải:

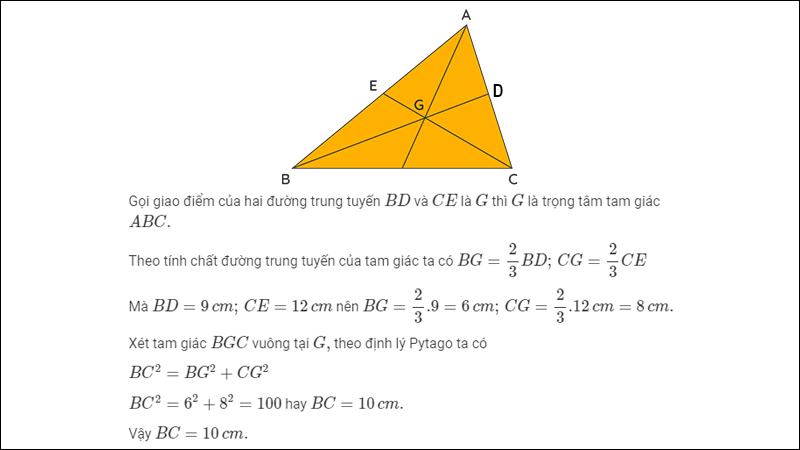
Bài 4:

Trong tam giác ABC, hai đường trung tuyến AA1 và BB1 cắt nhau tại điểm O. Hãy tính diện tích tam giác ABC nếu diện tích tam giác ABO  bằng 5cm2.

Lời giải:

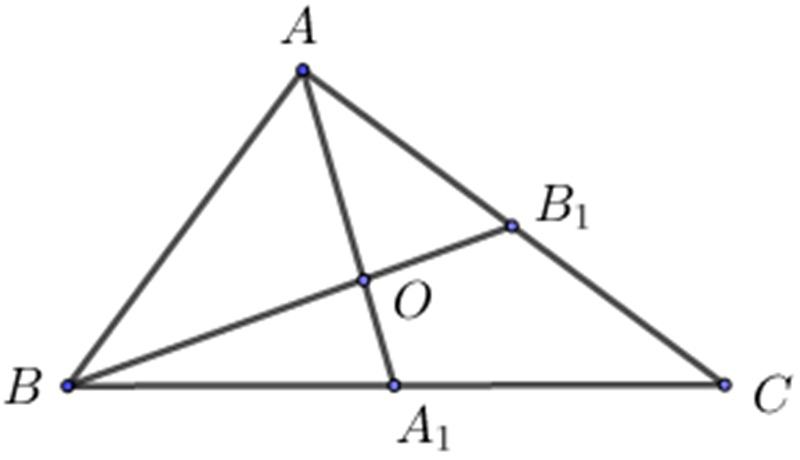
Ta có:

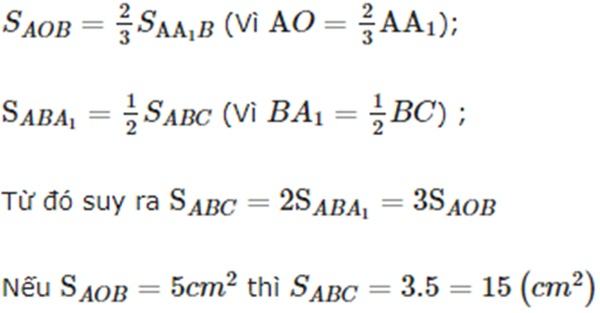
Bài 5:

Cho G là trọng tâm của tam giác DEF với đường trung tuyến DH.

Trong các khẳng định sau đây, khẳng định nào đúng?

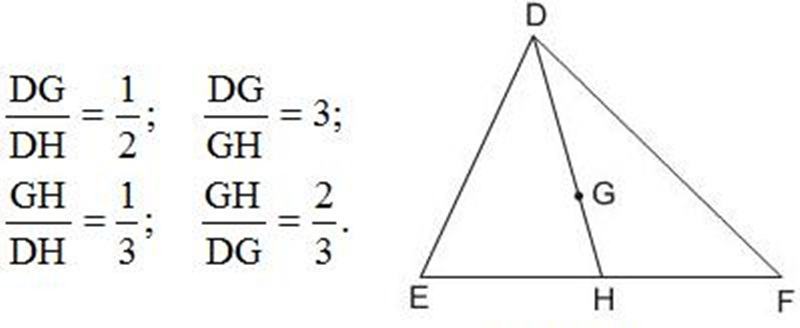
Lời giải:

Dạng 2: Đường trung tuyến với các tam giác đặc biệt

Đây là dạng toán đường trung tuyến ở các tam giác đặc biệt như tam giác cân, tam giác đều hay tam giác vuông. Khi gặp dạng toán như này, bạn cần lưu ý áp dụng tính chất đường trung tuyến như sau:

• Trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền thì bằng nửa cạnh huyền.
• Trong tam giác cân và tam giác đều, đường trung tuyến ứng với cạnh đáy và chia tam giác thành hai tam giác bằng nhau.

Bài tập ví dụ:

Bài 1:

Cho G là trọng tâm của tam giác đều ABC. Chứng minh rằng GA = GB = GC.

Lời giải:

Gọi D, E, F lần lượt là trung điểm cạnh BC, AB, AC.

Ta có:

• AD là đường trung tuyến trong tam giác ABC nên GA = ⅔. AD (1)
• BF là đường trung tuyến trong tam giác ABC nên GB = ⅔. BF (2)
• CE là đường trung tuyến trong tam giác ABC nên GC = ⅔. CE (3)

Vì ΔABC đều nên AD = BF = CE (4)

Từ (1), (2), (3), (4) suy ra GA = GB = GC

Bài 2: 

Cho tam giác vuông ABC có hai cạnh góc vuông AB = 3cm, AC = 4cm. Tính khoảng cách từ đỉnh A tới trọng tâm G của tam giác ABC.

Lời giải:

Gọi M là trung điểm của BC

Suy ra: AM là trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền

Nên AM=1/2. BC

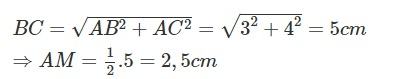
Vì G là trọng tâm của tam giác ABC nên AG=2/3. AM = 2/3. 2,5 = 1,7cm

Vậy AG =1,7cm.

Bài 3:

Cho tam giác DEF cân tại D với đường trung tuyến DI

a) Chứng minh ∆DEI  = ∆DFI

b) Các góc DIE và góc DIF là những góc gì?

c) Biết DE = DF = 13cm, EF = 10cm, hãy tính độ dài đường trung tuyến DI.

Lời giải:

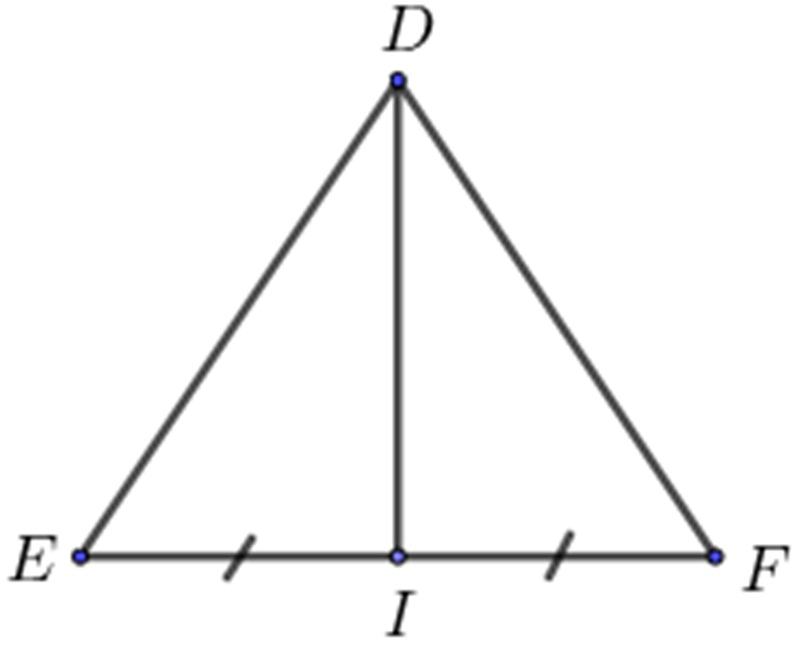
a) ∆DEI  = ∆DFI có:

DI là cạnh chung

DE = DF ( ∆DEF cân)

IE = IF (DI là trung tuyến)

⇒ ∆DEI  = ∆DFI (c.c.c)

b) Vì ΔDEI = ΔDFI ⇒ ∠DIE = ∠DIF

Mà ∠BID + ∠DIF=180 độ  (kề bù)

Nên ∠DIE = ∠DIF = 90 độ

c) I là trung điểm của EF nên IE = IF = 5cm

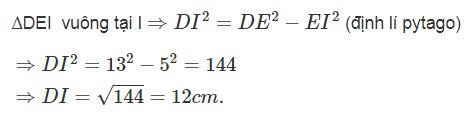
Bài 4:

Cho tam giác ABC cân ở A có AB = AC = 17cm, BC= 16cm. Kẻ trung tuyến AM.

a) Chứng minh: AM ⊥ BC;

b) Tính độ dài AM.

Lời giải:

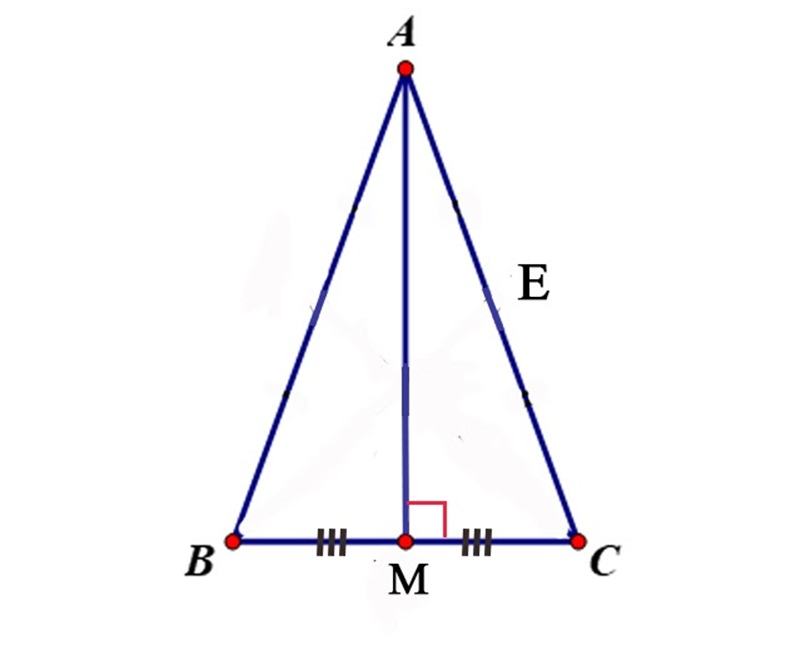
a) Ta có AM là đường trung tuyến ABC nên MB = MC

Mặt khác tam giác ABC cân tại A

⇒ AM vừa là đường trung tuyến vừa là đường cao.

Vậy AM ⊥ BC

b) Ta có:

BC = 16cm nên BM = MC = 8cm

AB = AC = 17cm

Xét tam giác AMC vuông tại M

Áp dụng Định lý Pitago có:

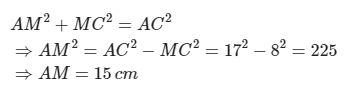
Như vậy qua bài viết hôm nay, Chúng Tôi đã cùng bạn ôn tập về lý thuyết và bài tập tính chất đường trung tuyến. Hy vọng bài viết trên có thể giúp ích cho bạn học tập hiệu quả hơn. Hẹn gặp lại bạn với những thông tin thú vị khác!