Bạn đang xem bài viết Tính chất đường phân giác trong tam giác? Lý thuyết & bài tập tại thcshuynhphuoc-np.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Đường phân giác trong tam giác là một đường thẳng đi qua một trong ba đỉnh của tam giác và chia tam giác thành hai phần có diện tích bằng nhau. Tính chất này là một trong những đặc điểm đáng chú ý và quan trọng trong lĩnh vực hình học tam giác.
Theo lý thuyết tam giác, một đường phân giác của tam giác ABC có thể được xác định bằng cách kết hợp hai cạnh không liên tiếp với nhau. Đúng như tên gọi, đường phân giác chia đôi tam giác và tạo thành hai tam giác con có diện tích bằng nhau.
Công thức cho diện tích tam giác con được tạo bởi đường phân giác là S = (1/2) * b * h, trong đó b là cạnh của tam giác gốc và h là chiều cao từ đỉnh tương ứng đến cạnh đó. Do đường phân giác chia tam giác thành hai phần có diện tích bằng nhau, ta có thể tìm ra độ dài đường phân giác bằng cách giải phương trình diện tích đồng dạng cho hai tam giác con.
Ngoài tính chất về diện tích, đường phân giác trong tam giác còn có một số tính chất khác đáng chú ý. Trong tam giác ABC, đường phân giác chia đôi góc BAC, tức là góc ADB = góc ADC. Điều này xảy ra bởi vì các tam giác ADB và ADC có cùng một góc D, cạnh AD và cạnh chung BD và CD.
Đối với bài tập, để áp dụng kiến thức về tính chất đường phân giác trong tam giác, ta có thể giải các bài tập liên quan đến tính diện tích, tìm giá trị của các góc hoặc các đoạn thẳng được tạo bởi đường phân giác trong tam giác. Ví dụ, cho hai cạnh và một góc trong một tam giác, ta có thể tìm đường phân giác tương ứng và tính toán các giá trị liên quan.
Tóm lại, tính chất đường phân giác trong tam giác không chỉ có vai trò quan trọng trong việc chia tam giác thành hai phần có diện tích bằng nhau, mà còn có những tính chất khác liên quan đến góc và cạnh của tam giác. Việc nắm vững lý thuyết và áp dụng vào các bài tập là một cách tốt để hiểu và khai thác tính chất đáng chú ý này.
Có lẽ khái niệm đường phân giác đã quá quen thuộc với những ai từng học qua chương trình trung học cơ sở rồi phải không nào? Vậy thì đường phân giác trong tam giác là gì? Lý thuyết tính chất đường phân giác trong tam giác là gì? Hãy cùng Chúng Tôi lướt ngay xuống bài viết dưới đây để tìm hiểu kĩ hơn nhé!
Tính chất đường phân giác trong tam giác
Để hiểu rõ hơn về khái niệm này, các bạn hãy cùng khám phá chi tiết hơn ngay sau đây nhé!
Định nghĩa đường phân giác trong tam giác
Đường phân giác trong tam giác là đường thẳng chia một góc của tam giác đó thành hai góc bằng nhau. Bên cạnh đó chúng ta còn biết được khái niệm ba đường phân giác của một tam giác. Trong một tam giác có 3 đường phân giác và chúng đồng quy với nhau tại 1 điểm. Điểm này cách đều ba cạnh của tam giác đó và được gọi là tâm đường tròn nội tiếp tam giác.
Ví dụ: trên có 3 đường phân giác được hạ từ 3 đỉnh A, B, C: AH, CP, BK và chúng giao nhau tại O.
Trường hợp đặc biệt hơn có thể xảy ra là đường phân giác trong tam giác cân. Trong tam giác cân, đường phân giác hạ từ đỉnh cân xuống cạnh đáy vừa là đường trung tuyến, đường trung trực, đường cao của tam giác đó.
Định lý đường phân giác trong tam giác
Định lý đường phân giác trong tam giác: Trong một tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề của hai đoạn ấy.
Ví dụ 1: Cho △ABC có AD là tia phân giác của góc A; D thuộc BC.
Vậy ta sẽ có tỉ lệ AB/AC=DB/DC (tính chất đường phân giác trong tam giác).
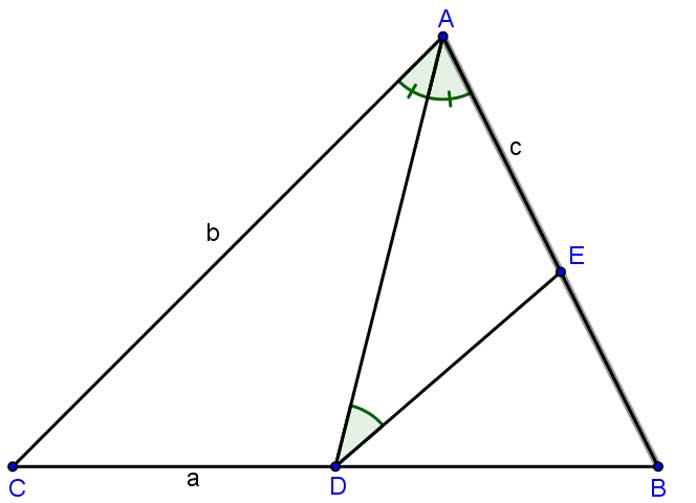
Ví dụ 2:
Cho tam giác có lần lượt là đường phân giác góc trong và góc ngoài tại đỉnh .
Khi đó ta có và
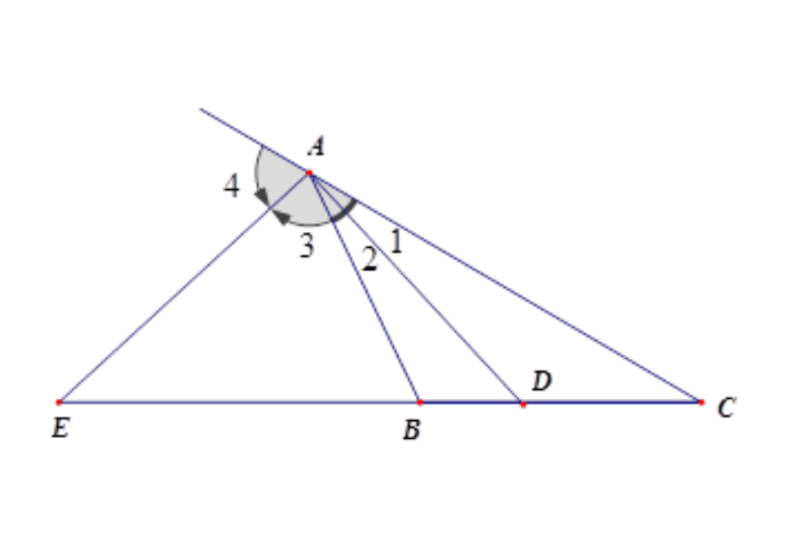
Những chú ý về đường phân giác trong tam giác
Bên cạnh những lý thuyết về đường phân giác trong tam giác, chúng ta cũng cần phải để ý một vài chú ý về khái niệm này. Trước tiên, định lí về đường phân giác trong tam giác vẫn đúng với đường phân giác góc ngoài của tam giác.
Ngoài ra, chúng ta nên chú ý vẽ hình sao cho thật chính xác, đặc biệt là vẽ đường phân giác trong tam giác. Ba đường phân giác trong tam giác đồng quy tại một điểm nên mọi người cần lưu ý trong việc vẽ hình.
Ví dụ:
AE’ là phân giác của góc BAx (AB ≠ AC).
Ta có: AB/AC = E’B/E’C hay E’B/AB = E’C/AC
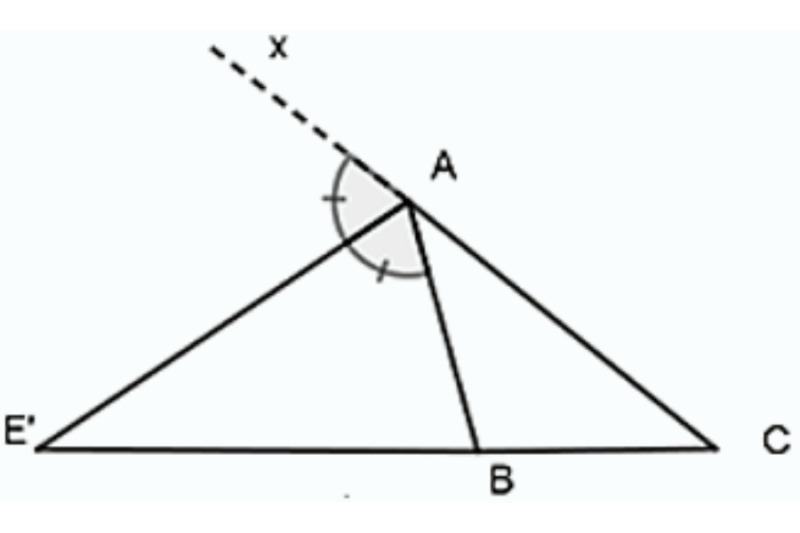
Chủ đề liên quan:
- Tính chất hình thang vuông? Bài tập về hình thang vuông
Bài tập về tính chất đường phân giác trong tam giác
Chúng ta hãy cùng nhau đi vào phần bài tập để nắm rõ hơn về kiến thức phần này nhé!
Bài 1: Cho hình thang ABCD (AB // CD).
Đường thẳng a song song với DC, cắt các cạnh AD và BC theo thứ tự là E và F.
Chứng minh rằng:
a) AE/ED = BF/FC.
b) AE/AD = BF/BC.
c) DE/DA = CF/CB.
Bài giải:
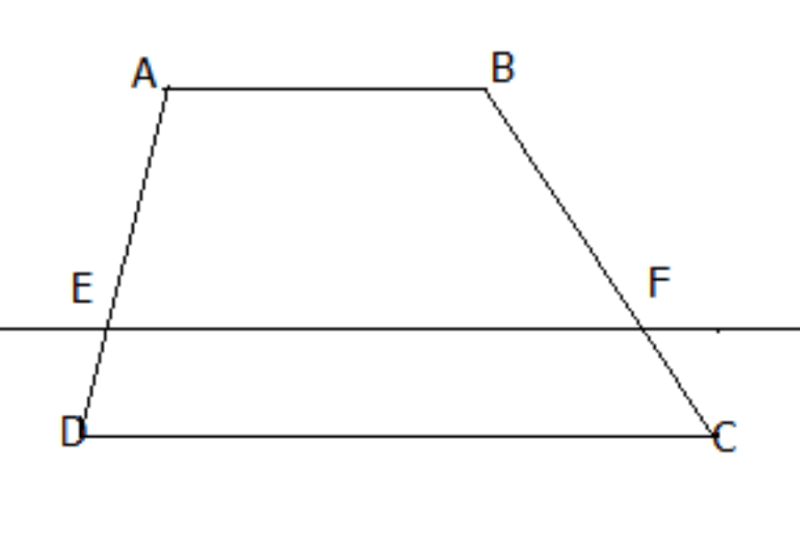 Áp dụng định lí Ta – lét, ta có:
Áp dụng định lí Ta – lét, ta có:
a) a // CD // AB
=> AE/ED = BF/FC (định lí Ta – lét)
b) a // CD // AB
=> AE/ED = BF/BC (định lí Ta – lét)
c) a // CD // AB
=> DE/DA = CF/CB (định lí Ta – lét).
Bài 2:
Cho tam giác ABC có AB = 5cm, AC = 6cm, BC = 7cm. Tia phân giác của góc BAC cắt BC tại E. Tính các đoạn EB, EC.
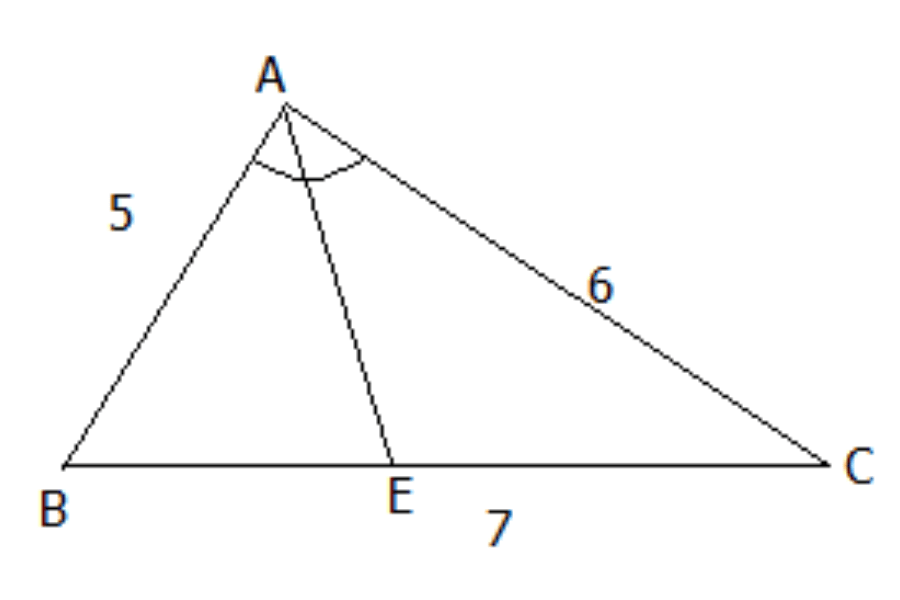
Bài giải:
Vì AE là đường phân giác của tam giác ABC nên ta có:
EB/EC = AB/AC = 5/6.
Do đó theo tính chất của dãy tỉ số bằng nhau, ta có:
EB/5 = EC/6 = (EB + EC)/(5 + 6) = 7/11.
Vì vậy ta có: EB/5 = 7/11.
=> EB = 5.(7/11) = 35/11 (cm).
Ta có: EC/6 = 7/11.
=> EC = 6.(7/11) = 42/11 (cm).
Bài 3: Cho tam giác ABC với đường trung tuyến AM. Tia phân giác của góc AMB cắt cạnh AB ở D, tia phân giác của góc AMC cắt cạnh AC ở E. Chứng minh rằng DE // BC.
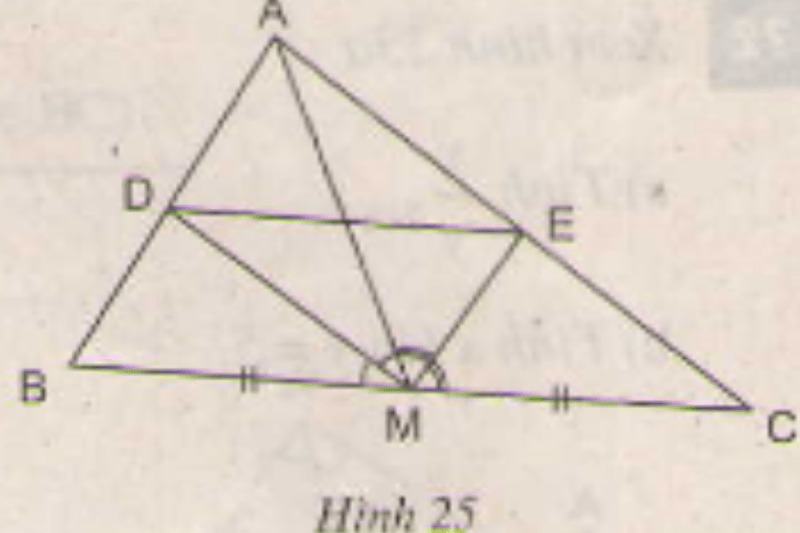
Ta có MD là đường phân giác của tam giác ABM
=> = (1)
ME là đường phân giác của tam giác ACM.
=> = (2)
Mà MB = MC (AM là đường trung tuyến)
=> = (3)
Từ 1, 2, 3 => = => DE // BC (Định lí Ta – lét đảo).
Qua bài viết trên, chắc hẳn các bạn cũng đã biết được các tính chất đường phân giác trong tam giác rồi phải không? Vậy thì còn chần chờ gì nữa, hãy theo dõi Chúng Tôi ngay để cập nhật thêm nhiều thông tin thú vị nhé!
Kiến thức hữu ích:
- Tính chất cơ bản của phân thức là gì? 3 Dạng toán cơ bản của phân thức
Trong tam giác, đường phân giác là đường thẳng đi qua một góc của tam giác và chia nó thành hai phần có tỉ lệ bằng nhau với tỉ lệ của hai cạnh góc đối diện. Tính chất của đường phân giác trong tam giác là một trong những khái niệm cơ bản được sử dụng rất phổ biến trong lý thuyết tam giác.
Đường phân giác trong tam giác có một số tính chất quan trọng. Đầu tiên, các đường phân giác của một tam giác gặp nhau tại một điểm gọi là trọng tâm. Trọng tâm của tam giác là trung điểm của ba đường phân giác. Điều này có nghĩa là đường phân giác chung đi qua trọng tâm của tam giác.
Thứ hai, đường phân giác chia tam giác thành hai phần có diện tích bằng nhau. Ý nghĩa của tính chất này là căn cứ trên diện tích tam giác, ta có thể xác định vị trí của đường phân giác và tính toán tỉ lệ diện tích của hai phần bằng cách sử dụng các công thức diện tích tam giác.
Cuối cùng, đường phân giác gặp cạnh tương ứng tại một điểm có tỉ lệ đúng với đột phân của hai cạnh góc đối diện. Tức là đường phân giác của một góc trong tam giác chia cạnh tương ứng thành hai phần có tỉ lệ bằng với đột phân của hai cạnh góc đối diện. Điều này rất hữu ích trong việc tìm các đoạn thẳng song song và chứng minh các đẳng thức tỉ lệ.
Trong thực tế, tính chất của đường phân giác trong tam giác được áp dụng rất nhiều trong các bài toán và trường hợp thực tế. Việc hiểu và sử dụng tính chất này giúp chúng ta giải quyết các bài tập tam giác một cách dễ dàng và chính xác.
Cảm ơn bạn đã xem bài viết Tính chất đường phân giác trong tam giác? Lý thuyết & bài tập tại thcshuynhphuoc-np.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Đường phân giác
2. Tam giác
3. Tính chất
4. Góc
5. Đỉnh
6. Đường cao
7. Đường trung bình
8. Tính chất đường phân giác trong tam giác vuông
9. Điểm giao nhau
10. Cạnh
11. Độ dài đường phân giác
12. Công thức tính đường phân giác
13. Tính chất đường phân giác trong tam giác đều
14. Bài tập về tính chất đường phân giác
15. Giải bài tập về tính chất đường phân giác trong tam giác


