Bạn đang xem bài viết Tâm đường tròn ngoại tiếp tam giác là gì? Bài tập vận dụng tại thcshuynhphuoc-np.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Tâm đường tròn ngoại tiếp tam giác là một khái niệm quan trọng trong hình học, có ứng dụng rộng rãi trong các bài toán và bài tập liên quan đến tam giác. Tâm đường tròn ngoại tiếp tam giác là một điểm duy nhất nằm trên đường tròn ngoại tiếp tam giác và khả năng chứa được tam giác bên trong nó.
Để hiểu rõ hơn về tâm đường tròn ngoại tiếp tam giác, chúng ta cần tìm hiểu về các khái niệm liên quan như đường tròn ngoại tiếp và tam giác. Đầu tiên, đường tròn ngoại tiếp tam giác là một đường tròn đi qua ba đỉnh của tam giác. Điều đặc biệt ở đây là đường tròn này được xác định bởi tam giác một cách duy nhất. Điểm tâm của đường tròn ngoại tiếp tam giác là tâm đường tròn ngoại tiếp tam giác.
Tâm đường tròn ngoại tiếp tam giác có rất nhiều tính chất quan trọng. Đầu tiên, tam giác có thể được tạo thành bởi ba đoạn thẳng nối các đỉnh của nó đến tâm đường tròn ngoại tiếp. Ngoài ra, hai giải thích cơ bản khác liên quan đến tâm đường tròn ngoại tiếp tam giác bao gồm: thì tâm đường tròn ngoại tiếp tam giác là nơi giao nhau của ba trục đối xứng qua các cạnh của tam giác và điểm tâm bảo toàn các độ dài bán kính ba đường tròn cắt tam giác.
Bài tập vận dụng về tâm đường tròn ngoại tiếp tam giác cũng rất phong phú và đa dạng. Các bài toán có thể yêu cầu chúng ta xác định vị trí của tâm đường tròn ngoại tiếp, tính toán các độ dài đoạn thẳng liên quan đến tâm đường tròn ngoại tiếp tam giác hoặc tìm các mối quan hệ giữa các tam giác ngoại tiếp cùng một đường tròn. Trong quá trình giải quyết các bài tập này, chúng ta có cơ hội nắm vững các tính chất và quy tắc liên quan đến tâm đường tròn ngoại tiếp tam giác, từ đó mở rộng kiến thức về hình học và ứng dụng của nó trong thực tế.
Tóm lại, tâm đường tròn ngoại tiếp tam giác không chỉ là một khái niệm hình học quan trọng mà còn có thể được áp dụng trong nhiều bài toán thực tế. Hiểu rõ về tâm đường tròn ngoại tiếp tam giác sẽ giúp chúng ta cải thiện khả năng giải quyết các bài toán hình học phức tạp và phát triển tư duy logic trong việc áp dụng các quy tắc và tính chất của nó vào thực tế.
Tất cả những kiến thức liên quan đến đường tròn đều là những kiến thức rất quan trọng và cần phải nắm vững. Bài viết này của Chúng Tôi sẽ giải đáp thắc mắc của bạn về tâm đường tròn ngoại tiếp tam giác là gì nhé!
Tâm đường tròn ngoại tiếp tam giác là gì?
Đường tròn ngoại tiếp tam giác là gì?
Đường tròn ngoại tiếp tam giác là đường tròn mà đi qua ba đỉnh của một hình tam giác. Trong trường hợp này, hình tam giác sẽ nội tiếp hình tròn.
Đường tròn ngoại tiếp tam giác là đường tròn mà có tâm là giao điểm của ba đường trung trực của tam giác đó.
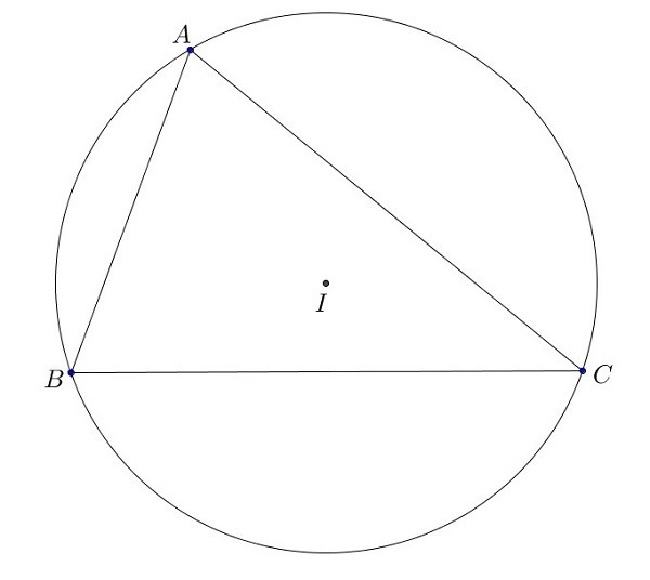
Tâm đường tròn ngoại tiếp tam giác là gì?
Tâm đường tròn ngoại tiếp tam giác là giao điểm của hai hoặc ba đường trung trực của tam giác đó. Hay nói cách khác là giao điểm của các đường trung trực của một tam giác chính là tâm của đường tròn ngoại tiếp tam giác.
Sau khi đã hiểu rõ về tâm đường tròn ngoại tiếp tam giác là gì thì hãy cùng Chúng Tôi tìm hiểu về những tính chất của tâm đường tròn ngoại tiếp tam giác là gì nhé!
Tính chất tâm đường tròn ngoại tiếp tam giác
Tâm đường tròn ngoại tiếp tam giác có những tính chất như sau:
- Mỗi một hình tam giác thì chỉ có duy nhất một đường tròn ngoại tiếp.
- Tâm của đường tròn ngoại tiếp chính là giao điểm của hai hoặc ba đường trung trực của tam giác.
- Tâm đường tròn ngoại tiếp tam giác vuông chính là trung điểm của cạnh huyền.
- Tâm đường tròn nội tiếp và ngoại tiếp tam giác sẽ trùng nhau nếu trong một tam giác đều.
Xem thêm:
- Bán kính đường tròn ngoại tiếp tam giác là gì? Khái niệm
- Tính chất tứ giác nội tiếp? Các dạng bài tập về tính chất nội tiếp
- Sự xác định đường tròn – tính chất đối xứng của đường tròn
Cách xác định tâm đường tròn ngoại tiếp tam giác
Muốn xác định được tâm đường tròn ngoại tiếp tam giác thì các bạn phải nhớ rằng tâm đường tròn ngoại tiếp tam giác chính là giao điểm của hai hoặc ba đường trung trực của tam giác đó.
Có hai cách để xác định tâm đường tròn ngoại tiếp tam giác như sau:
Cách 1:
Bước 1: Viết phương trình của đường trung trực hai cạnh bất kỳ của một tam giác.
Bước 2: Tìm được giao điểm hai đường trung trực. Giao điểm của các đường trung trực chính là tâm đường tròn ngoại tiếp tam giác.
Cách 2:
Bước 1: Gọi I (x, y) là tâm đường tròn ngoại tiếp tam giác ABC. Ta có IA = IB = IC = R (trong đó R là bán kính).
Bước 2: Tìm được tọa độ của tâm đường tròn ngoại tiếp tam giác.
Tọa độ tâm I là nghiệm của phương trình:
IA^2=IB^2
IA^2=IC^2
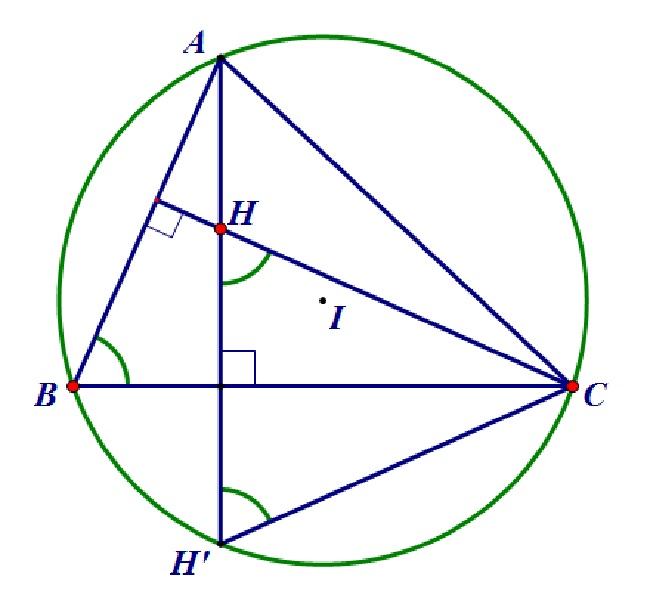
Bán kính tâm đường tròn ngoại tiếp tam giác
Bán kính tâm đường tròn ngoại tiếp tam giác
Trong một tam giác ABC nội tiếp đường tròn có các cạnh lần lượt là a,b,c. Chúng ta có công thức tính bán kính tâm đường tròn ngoại tiếp tam giác cho diện tích là S như sau:
R = (a x b x c) / 4S
Trong đó:
R là bán kính tâm đường tròn ngoại tiếp tam giác.
a,b,c là cạnh của hình tam giác.
S là diện tích tam giác.
Bán kính tâm đường tròn ngoại tiếp góc A
Công thức tính bán kính tâm đường tròn ngoại tiếp góc A như sau:
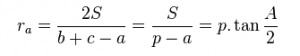
Trong đó:
a,b,c là các cạnh của tam giác nội tiếp đường tròn.
S là diện tích tam giác.
p là chu vi
Bán kính tâm đường tròn ngoại tiếp góc B
Công thức tính bán kính tâm đường tròn ngoại tiếp góc B như sau:
![]()
Trong đó:
a,b,c là các cạnh của một tam giác.
S là diện tích tam giác.
p là chu vi.
Bán kính tâm đường tròn ngoại tiếp góc C
Công thức tính bán kính tâm đường tròn ngoại tiếp góc C như sau:
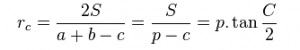
Trong đó:
a,b,c là các cạnh của một tam giác.
S là diện tích tam giác.
p là chu vi.
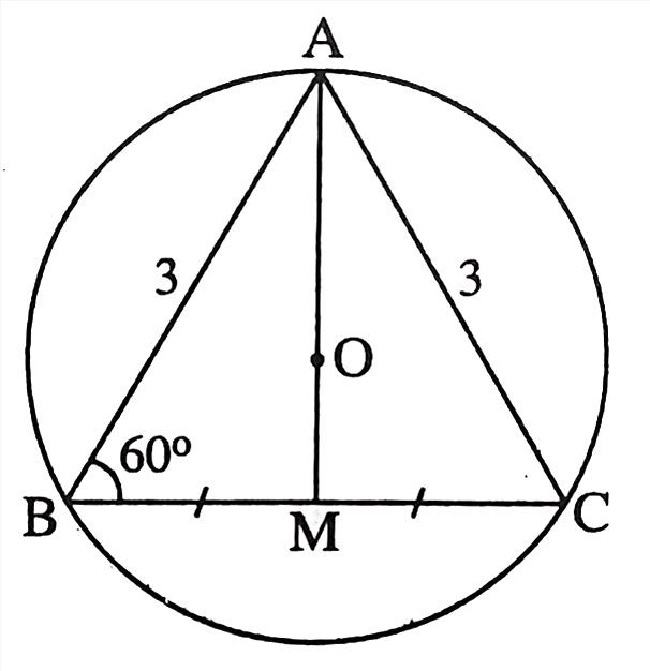
Bán kính tâm đường tròn tam giác đều
Công thức tính bán kính tâm đường tròn ngoại tiếp tam giác đều như sau:
R = a / (2 x sin60 độ)
Trong đó:
a là độ dài các cạnh của tam giác đều.
Bài tập về đường tròn ngoại tiếp tam giác
Dạng 1: Viết phương trình đường tròn nội tiếp tam giác ABC khi biết tọa độ 3 đỉnh
Ví dụ: Viết phương trình đường tròn ngoại tiếp tam giác A, B, C biết A(-1;2); B(6;1); C(-2;5)
Cách giải của dạng này như sau:
Gọi phương trình đường tròn ngoại tiếp có dạng:
![]()
Vì các đỉnh A, B, C cùng nằm trong một đường tròn nên thay tọa độ A, B, C lần lượt vào phương trình đường tròn (C) ta được hệ phương trình như sau:
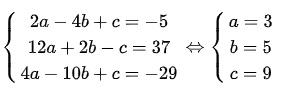
Vì vậy, phương trình đường tròn ngoại tiếp tam giác ABC có tâm I (3;5) bán kính R = 5 là:
![]()
Dạng 2: Tìm tâm của đường tròn ngoại tiếp khi biết tọa độ ba đỉnh
Ví dụ: Cho tam giác ABC với các tọa độ lần lượt là A(1;2), B(-1;0), C(3;2). Tìm tọa độ tâm của đường tròn ngoại tiếp tam giác ABC?
Cách giải của dạng toán này như sau:
Gọi I(x;y) là tâm đường tròn ngoại tiếp tam giác ABC
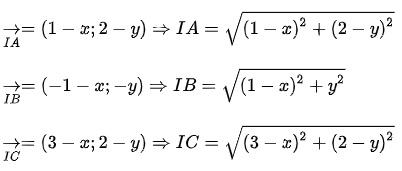
Do I là tâm đường tròn ngoại tiếp tam giác ABC nên:
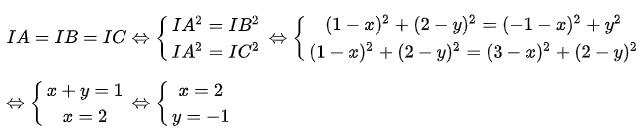
Vậy tọa độ tâm của đường tròn ngoại tiếp tam giác ABC là I(2;-1)
Dạng 3: Tìm bán kính đường tròn nội tiếp tam giác
Ví dụ: Tam giác ABC có cạnh AB = 3, AC = 7, BC = 8. Tính bán kính đường tròn ngoại tiếp tam giác ABC?
Cách giải của dạng toán này như sau:
Ta có:
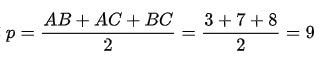
Áp dụng công thức Herong ta có:
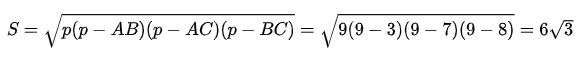
Vậy bán kính đường tròn ngoại tiếp tam giác là:
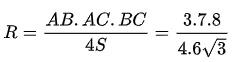
Bài tập vận dụng
Bài tập 1: Cho tam giác MNP vuông tại N, và MN = 6cm, NP = 8cm. Xác định bán kính đường tròn ngoại tiếp tam giác MNP bằng bao nhiêu?
Trả lời:
Áp dụng định lý Pytago trong tam giác vuông ta có:
PQ = 1/2 MP => NQ = QM = QP = 5cm.
Gọi D là trung điểm của đoạn thẳng MP
=> ∆MNP vuông tại N, có NQ là đường trung tuyến ứng với cạnh huyền MP.
=> Q là tâm đường tròn ngoại tiếp ∆MNP.
Vậy đường tròn ngoại tiếp ∆MNP có tâm Q của cạnh huyền MP và bán kính R = MQ = 5cm.
Bài tập 2: Cho tam giác ABC đều với cạnh bằng 6cm. Xác định tâm và bán kính của đường tròn ngoại tiếp tam giác ABC?
Trả lời:
Gọi D, E lần lượt là trung điểm của cạnh BC, AB. Ta có AD giao với CE tại O.
Ta có: Tam giác ABC là tam giác đều
=> Đường trung tuyến cũng là đường cao, đường phân giác và là đường trung trực của tam giác.
Vậy O là tâm đường tròn ngoại tiếp tam giác.
∆ABC có CE là đường trung tuyến
=> CE cũng là đường cao.
Áp dụng định lí Pytago vào tam giác vuông AEC có:
CE2 = AC2 – AE2 = 62 – 32 = 27 => CE =3√3cm.
Ta có: O là trọng tâm của tam giác ABC
=> CO = 2/3 CE = (2/3)3√3 = 2√3cm.
Vậy tâm đường tròn ngoại tiếp tam giác ABC là trọng tâm O và bán kính là OC = 2√3cm
Bài tập 3: Cho tam giác ABC cân tại A. Các đường cao AD, BE và CF cắt nhau tại H. Chứng minh tứ giác AEHF là tứ giác nội tiếp. Xác định tâm I của đường tròn ngoại tiếp tứ giác đó.
Trả lời:
Gọi I là trung điểm của AH
Ta có HF vuông góc với AF
=> tam giác AFH vuông tại F
I là trung điểm của cạnh huyền AH
=> IA = IF = IH (1)
Lại có HE vuông góc với AE
=> tam giác AEH vuông tại E
I là trung điểm của cạnh huyền AH
=> IA = IE = IH (2)
Từ (1) và (2) ta có IA = IF = IH = IE
Vậy tứ giác AEHF nội tiếp đường tròn có tâm I là trung điểm của AH.
Trên đây là toàn bộ thông tin liên quan đến kiến thức tâm đường tròn nội tiếp tam giác là gì. Hy vọng bài viết này đã giải đáp được những thắc mắc của bạn. Hãy theo dõi Chúng Tôi mỗi ngày để biết thêm nhiều thông tin hay và bổ ích nhé!
Trong toán học, tâm đường tròn ngoại tiếp tam giác là một điểm nằm trên đường tròn ngoại tiếp của tam giác và cách ba đỉnh của tam giác đều có cùng khoảng cách. Tâm đường tròn ngoại tiếp tam giác thường được ký hiệu là O và có các tính chất đặc biệt.
Một trong những tính chất quan trọng của tâm đường tròn ngoại tiếp tam giác là nó là trung điểm của đoạn thẳng nối hai đỉnh bất kỳ của tam giác với tâm đường tròn nội tiếp tam giác. Nghĩa là, tâm đường tròn ngoại tiếp tam giác nằm trên trọng tâm của tam giác.
Bên cạnh đó, tâm đường tròn ngoại tiếp tam giác cũng có tính chất nằm trên đường trung trực của các cạnh tam giác. Điều này có nghĩa là tâm đường tròn ngoại tiếp tam giác là tâm quay của tam giác khi thực hiện phép quay đều qua 360 độ.
Việc hiểu và áp dụng khái niệm về tâm đường tròn ngoại tiếp tam giác là rất quan trọng trong giải các bài toán liên quan đến tam giác. Ví dụ, thông qua việc tính toán và vận dụng tính chất của tâm đường tròn ngoại tiếp, chúng ta có thể tìm ra các giá trị góc, cạnh, hoặc vị trí tương đối giữa các đỉnh của tam giác. Điều này giúp giải quyết các bài toán như tính diện tích tam giác, tìm tọa độ các đỉnh tam giác, hay chứng minh những quan hệ toán học giữa các hình học học và tâm đường tròn ngoại tiếp tam giác.
Tóm lại, khái niệm về tâm đường tròn ngoại tiếp tam giác là một công cụ quan trọng và hữu ích trong việc giải quyết các bài toán liên quan đến tam giác. Việc hiểu và áp dụng đúng tính chất của tâm đường tròn ngoại tiếp tam giác sẽ giúp chúng ta có những cách tiếp cận hiệu quả và chính xác khi giải quyết các bài toán hình học.
Cảm ơn bạn đã xem bài viết Tâm đường tròn ngoại tiếp tam giác là gì? Bài tập vận dụng tại thcshuynhphuoc-np.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Tâm đường tròn ngoại tiếp tam giác
2. Đường tròn ngoại tiếp tam giác
3. Trung điểm đường tròn ngoại tiếp tam giác
4. Tính chất đường tròn ngoại tiếp tam giác
5. Tam giác nội tiếp đường tròn
6. Tâm đường tròn nội tiếp tam giác
7. Đường cao tam giác và đường tròn ngoại tiếp
8. Bán kính đường tròn ngoại tiếp tam giác
9. Tính chất bán kính đường tròn ngoại tiếp tam giác
10. Tính chất tâm đường tròn ngoại tiếp tam giác vuông
11. Bài tập vận dụng tâm đường tròn ngoại tiếp tam giác
12. Bài toán ứng dụng tâm đường tròn ngoại tiếp tam giác
13. Giải bài toán sử dụng tâm đường tròn ngoại tiếp tam giác
14. Tính toán bán kính đường tròn ngoại tiếp tam giác
15. Ví dụ vận dụng tâm đường tròn ngoại tiếp tam giác


