Bạn đang xem bài viết Công thức tính diện tích tam giác, hình tròn, hình vuông, hình chữ nhật, hình thang, hình bình hành tại thcshuynhphuoc-np.edu.vn bạn có thể truy cập nhanh thông tin cần thiết tại phần mục lục bài viết phía dưới.
Để tính diện tích các hình học như tam giác, hình tròn, hình vuông, hình chữ nhật, hình thang, hình bình hành, chúng ta cần sử dụng các công thức phù hợp. Công thức này giúp chúng ta tính toán diện tích một cách chính xác và nhanh chóng. Bên dưới là một số công thức phổ biến được sử dụng trong tính diện tích các hình học này.
Đối với tam giác, công thức tính diện tích là: Diện tích = (1/2) x cơ sở x chiều cao. Đây là một công thức đơn giản, với cơ sở là đoạn thẳng nối hai đỉnh của tam giác và chiều cao là khoảng cách từ đỉnh không thuộc cơ sở đến đường thẳng cơ sở.
Đối với hình tròn, công thức tính diện tích là: Diện tích = π x bán kính^2. π là một hằng số xấp xỉ 3.14 và bán kính là khoảng cách từ tâm đến bất kỳ điểm nào trên đường viền của hình tròn.
Đối với hình vuông, công thức tính diện tích là: Diện tích = cạnh^2. Đây là một công thức đơn giản, với cạnh là độ dài một cạnh của hình vuông.
Đối với hình chữ nhật, công thức tính diện tích là: Diện tích = chiều dài x chiều rộng. Đây là một công thức đơn giản, với chiều dài là độ dài một cạnh dọc của hình chữ nhật và chiều rộng là độ dài một cạnh ngang của hình chữ nhật.
Đối với hình thang, công thức tính diện tích là: Diện tích = (đáy lớn + đáy nhỏ) x chiều cao / 2. Đây là một công thức dựa trên sự kết hợp của đáy lớn, đáy nhỏ và chiều cao của hình thang.
Đối với hình bình hành, công thức tính diện tích là: Diện tích = cạnh x chiều cao. Công thức này tương tự công thức tính diện tích hình chữ nhật, với cạnh là độ dài một cạnh của hình bình hành và chiều cao là khoảng cách từ đỉnh không thuộc cạnh đến đường thẳng song song với cạnh đó.
Mỗi công thức trên đều mang đến một cách tính diện tích chính xác và dễ dùng cho từng loại hình học. Bằng cách áp dụng công thức đúng cho hình cần tính, chúng ta có thể tìm ra diện tích một cách nhanh chóng và chính xác.
Tính diện tích là các bài toán điển hình thường gặp trong các bài toán hình học kể cả hình học phẳng và hình học không gian. Từ cấp 1, cấp 2, cấp 3 và cả trong chương trình thi đại học hay bữa nay gọi là kỳ thi THPT quốc gia thì tính diện tích là một bước quan trọng trong các câu tính thể tích hình lăng trụ, hình chóp. Tuy không nhiều nhưng để lấy trọn vẹn số điểm trong các câu hỏi này thì chúng ta phải nhớ các công thức đã được học trong chương trình lớp dưới. Vì các câu này không quá khó nên nếu không may quên công thức mà không thể làm được thì mất điểm không đáng. Sau đây chúng tôi sẽ tổng hợp lại các công thức tính diện tích của các hình tam giác và các hình tứ giác đặc biệt như: hình vuông, hình chữ nhật, hình thang… để các em học sinh có phương tiện dễ dàng học tập và ôn luyện.
Công thức tính diện tích tam giác, hình tròn và các tứ giác: hình vuông, hình chữ nhật, hình thang, hình bình hành
- Công thức tính diện tích tam giác
- Tam giác thường
Cho tam giác ABC với độ dài các cạnh như hình vẽ. Tính diện tích tam giác ABC ?

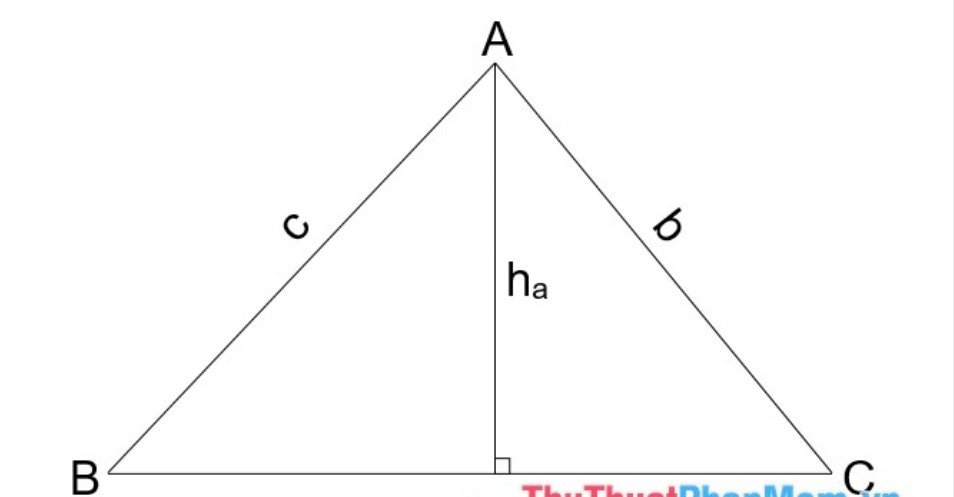
Khi đó, để tính diện tích tam giác ABC, ta có thể sử dụng một trong các công thức sau đây:






- Tam giác vuông

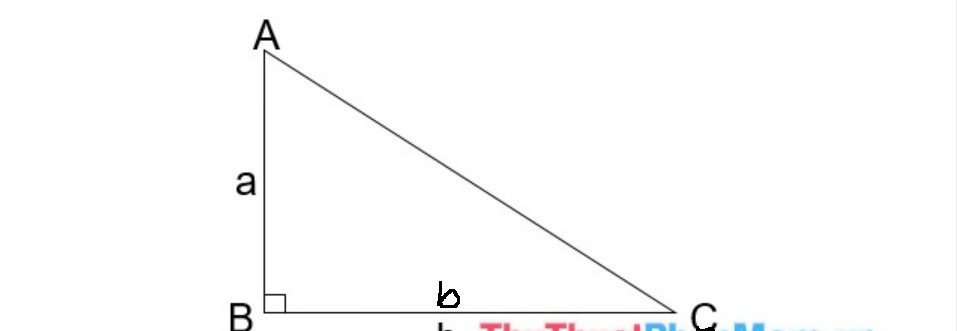


- Tam giác cân

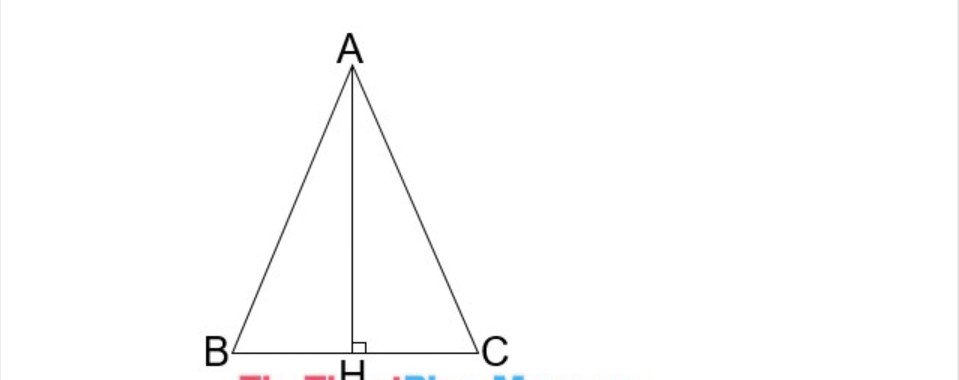


- Tam giác đều


2. Công thức tính diện tích, chu vi hình tròn
- Diện tích hình tròn



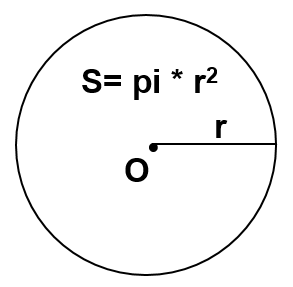
- Công thức tính chu vi hình tròn


3. Công thức tính diện tích các tứ giác đặc biệt
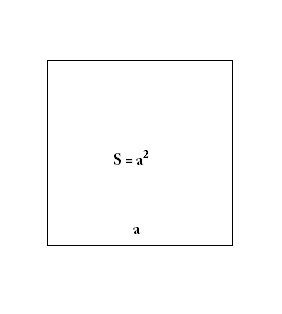
- Hình vuông: Cho hình vuông cạnh a, tính diện tích hình vuông đó?
Diện tích hình vuông bằng bình phương độ dài cạnh a. S=a^2

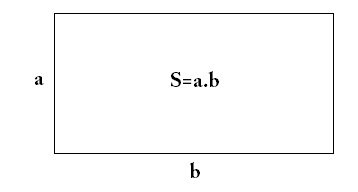
- Hình chữ nhật
Hình chữ nhật có chiều rộng là a, chiều dài là b. Khi đó, công thức tính diện tích hình chữ nhật bằng tích chiều dài nhân chiều rộng. S=a.b

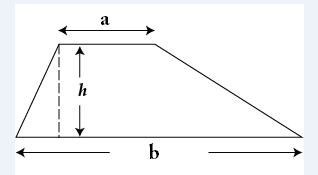
- Hình thang
Hình thang bên dưới có a là độ dài đáy bé, b là độ dài đáy lớn và h là chiều cao của hình thang. Khi đó, muốn tính diện tích hình thang ta tính theo công thức sau:

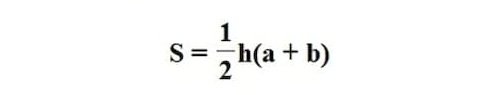

Công thức tính diện tích hình thang được các em cấp 1 đọc thành thơ để dễ thuộc, đây cũng là một cách học rất hay:
“Muốn tính diện tích hình thang,
ta lấy đáy lớn, đáy bé ta mang cộng vào
Thế rồi nhân với chiều cao,
chia đôi lấy nửa thế nào cũng ra”
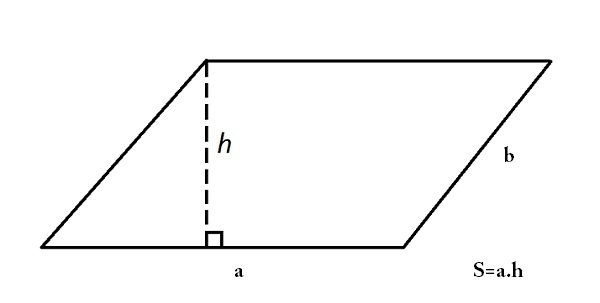
- Hình bình hành:
Hình bình hành có 2 cạnh a, b và chiều cao h. Diện tích hình bình hành được tính bằng cách lấy tích của cạnh a và đường cao h hạ xuống cạnh a. S=a.h

Trên đây là công thức tính diện tích tam giác, hình tròn và các tứ giác đặc biệt do tindep.com tổng hợp. Qua bài viết này chúng tôi gợi lại cho các em nhớ lại các công thức tính diện tích của các hình thường gặp mà các em đã được học, hi vọng bài viết này sẽ giúp ích nhiều cho các em. Và rất nhiều các công thức khác được tổng hợp và chia sẻ; thường xuyên truy cập trang để có thêm nhiều kiến thức mới nhé! Chúc các bạn học sinh học tập tốt!
Công thức tính diện tích các hình học là những kiến thức cơ bản trong toán học, rất quan trọng và có ứng dụng rộng rãi trong cuộc sống hàng ngày. Trong bài viết này, chúng ta đã tìm hiểu về công thức tính diện tích của các hình học phổ biến như tam giác, hình tròn, hình vuông, hình chữ nhật, hình thang và hình bình hành.
Công thức tính diện tích tam giác là bán kính nhân đường cao chia đôi, hay gấp đôi tích cạnh đáy và đường cao tương ứng. Đối với hình tròn, công thức tính diện tích là bán kính mũ hai nhân pi. Công thức tính diện tích hình vuông là cạnh nhân chính mũ hai. Trong trường hợp hình chữ nhật, công thức là tích hai cạnh đáy và chiều cao, có thể cũng được tính bằng cách nhân đường chéo lớn và nhỏ chia đôi. Đối với hình thang, công thức tính diện tích là tích tổng hai đáy và chiều cao, rồi chia đôi. Cuối cùng, công thức tính diện tích hình bình hành là tích cạnh đáy và đường cao đi qua cạnh đáy.
Việc nắm vững công thức tính diện tích các hình học này sẽ giúp chúng ta áp dụng vào các bài toán thực tế, như tính diện tích một mảnh đất, diện tích một chiếc tấm bảng hay diện tích một khu vườn. Ngoài ra, việc hiểu về công thức tính diện tích cũng giúp chúng ta phát triển tư duy logic và khả năng giải quyết vấn đề.
Tuy nhiên, cần lưu ý rằng công thức chỉ là công cụ để tính toán, và không phải là cách duy nhất để giải quyết một bài toán. Đôi khi, việc sử dụng cách tính diện tích thông qua đồ thị hình học hoặc phân tích không gian cũng được áp dụng. Quan trọng nhất là hiểu rõ ý nghĩa của diện tích và biết áp dụng nó vào các tình huống khác nhau.
Tổng kết lại, công thức tính diện tích các hình học là những kiến thức cần thiết để giải quyết các bài toán liên quan đến quy mô không gian. Nắm vững và hiểu rõ cách sử dụng công thức này không chỉ giúp chúng ta tính toán hiệu quả, mà còn phát triển tư duy logic và khả năng giải quyết vấn đề.
Cảm ơn bạn đã xem bài viết Công thức tính diện tích tam giác, hình tròn, hình vuông, hình chữ nhật, hình thang, hình bình hành tại thcshuynhphuoc-np.edu.vn bạn có thể bình luận, xem thêm các bài viết liên quan ở phía dưới và mong rằng sẽ giúp ích cho bạn những thông tin thú vị.
Từ Khoá Liên Quan:
1. Diện tích tam giác
2. Công thức tính diện tích tam giác
3. Diện tích hình tròn
4. Công thức tính diện tích hình tròn
5. Diện tích hình vuông
6. Công thức tính diện tích hình vuông
7. Diện tích hình chữ nhật
8. Công thức tính diện tích hình chữ nhật
9. Diện tích hình thang
10. Công thức tính diện tích hình thang
11. Diện tích hình bình hành
12. Công thức tính diện tích hình bình hành
13. Bài toán tính diện tích tam giác
14. Bài toán tính diện tích hình tròn
15. Bài toán tính diện tích hình vuông

